备考2022届中考数学全国精选题汇编专题6 函数图象及性质(1)
试卷更新日期:2022-02-21 类型:一轮复习
一、单选题
-
1. 某同学将如图所示的三条水平直线 , , 的其中一条记为x轴(向右为正方向),三条竖直直线 , , 的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数的图象,那么她所选择的x轴和y轴分别为直线( )
 A、 , B、 , C、 , D、 ,2. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A、 , B、 , C、 , D、 ,2. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( ) A、22 B、24 C、 D、3. 在平面直角坐标系 中,对于点 和 ,给出如下定义:若 ,则称点Q为点P的“可控变点”.例如:点 的“可控变点”为点 ,点 的“可控变点”为点 .若点P在函数 的图象上,则其“可控变点”Q的纵坐标 关于x的函数图象大致正确的是( )A、
A、22 B、24 C、 D、3. 在平面直角坐标系 中,对于点 和 ,给出如下定义:若 ,则称点Q为点P的“可控变点”.例如:点 的“可控变点”为点 ,点 的“可控变点”为点 .若点P在函数 的图象上,则其“可控变点”Q的纵坐标 关于x的函数图象大致正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知二次函数 的图象上有点 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、5. 如图所示是函数 的部分图象,与x轴交于点 ,对称轴是直线 .下列结论:
4. 已知二次函数 的图象上有点 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、5. 如图所示是函数 的部分图象,与x轴交于点 ,对称轴是直线 .下列结论:
(1) ;(2) ;(3)当 时, ;(4) ,( 为任意实数).其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个6. 下列关于反比例函数 ,说法不正确的是( )A、点(-2,1)、(-1,2)均在其图象上 B、双曲线分布在二、四象限 C、该函数图象上有两点A 、B ,若 < ,则 < D、当 时,x的范围是0 < x < 17. 已知点 , , 三点都在反比例函数 的图象上,则下列关系正确的是( )A、 B、 C、 D、8. 下列函数中,① ;② ;③ ;④ .函数图象经过第四象限的有( )A、1个 B、2个 C、3个 D、4个9. 已知点 均在抛物线 上,其中 .若 ,则m的取值范围是( )A、 B、 C、 D、10. 点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )A、4 B、-4 C、-4.5 D、4.511. 如图,A为反比例函数y= (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=6.连接OA,AB,且OA=AB.过点B作BC⊥OB,交反比例函数y= (其中x>0)的图象于点C,连接OC交AB于点D,S△OBC=6,则AB的长度为( )
A、1个 B、2个 C、3个 D、4个6. 下列关于反比例函数 ,说法不正确的是( )A、点(-2,1)、(-1,2)均在其图象上 B、双曲线分布在二、四象限 C、该函数图象上有两点A 、B ,若 < ,则 < D、当 时,x的范围是0 < x < 17. 已知点 , , 三点都在反比例函数 的图象上,则下列关系正确的是( )A、 B、 C、 D、8. 下列函数中,① ;② ;③ ;④ .函数图象经过第四象限的有( )A、1个 B、2个 C、3个 D、4个9. 已知点 均在抛物线 上,其中 .若 ,则m的取值范围是( )A、 B、 C、 D、10. 点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )A、4 B、-4 C、-4.5 D、4.511. 如图,A为反比例函数y= (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=6.连接OA,AB,且OA=AB.过点B作BC⊥OB,交反比例函数y= (其中x>0)的图象于点C,连接OC交AB于点D,S△OBC=6,则AB的长度为( )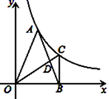 A、4 B、5 C、5 D、512. 如图,在平面直角坐标系中,以坐标原点 , , 为顶点的 ,其两个锐角对应的外角角平分线相交于点 ,且点 恰好在反比例函数 的图象上,则 的值为( )
A、4 B、5 C、5 D、512. 如图,在平面直角坐标系中,以坐标原点 , , 为顶点的 ,其两个锐角对应的外角角平分线相交于点 ,且点 恰好在反比例函数 的图象上,则 的值为( )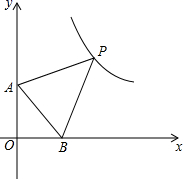 A、25 B、36 C、49 D、6413. 双曲线 有三个点 , , ,若 ,则 , , 的大小关系是( )A、 B、 C、 D、14. 如图5,在反比例函数 的图象上有一动点 ,连接 并延长交图象的另一支于点 ,在第一象限内有一点C,满足 ,当点 运动时,点 始终在函数 的图象上运动,若 ,则 的值为( )
A、25 B、36 C、49 D、6413. 双曲线 有三个点 , , ,若 ,则 , , 的大小关系是( )A、 B、 C、 D、14. 如图5,在反比例函数 的图象上有一动点 ,连接 并延长交图象的另一支于点 ,在第一象限内有一点C,满足 ,当点 运动时,点 始终在函数 的图象上运动,若 ,则 的值为( )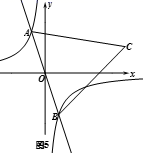 A、2 B、4 C、6 D、815. 已知关于 的一次函数为 ,那么这个函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限16. 正比例函数 和反比例函数 的图象如图所示,交点 的坐标是 ,那么当 时, 的取值范围是( )
A、2 B、4 C、6 D、815. 已知关于 的一次函数为 ,那么这个函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限16. 正比例函数 和反比例函数 的图象如图所示,交点 的坐标是 ,那么当 时, 的取值范围是( )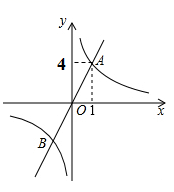 A、 B、 C、 D、 或17. 如图, 的圆心 的坐标为 ,半径为1,直线 的表达式为 , 是直线 上的动点, 是 上的动点,则 的最小值是( )
A、 B、 C、 D、 或17. 如图, 的圆心 的坐标为 ,半径为1,直线 的表达式为 , 是直线 上的动点, 是 上的动点,则 的最小值是( )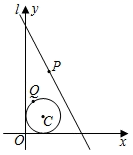 A、 B、 C、 D、18. 对于一次函数 ,下列说法不正确的是( )A、图象经过点 B、图象与x轴交于点 C、图象不经过第四象限 D、当 时,19. 如图,已知△ABC是等腰直角三角形,∠ABC=90°,A点坐标(-2,0),B点坐标为(1,1),点C在反比例函数 上,则k的值为( )
A、 B、 C、 D、18. 对于一次函数 ,下列说法不正确的是( )A、图象经过点 B、图象与x轴交于点 C、图象不经过第四象限 D、当 时,19. 如图,已知△ABC是等腰直角三角形,∠ABC=90°,A点坐标(-2,0),B点坐标为(1,1),点C在反比例函数 上,则k的值为( ) A、 B、 C、-4 D、-220. 关于抛物线 ,下列结论中不正确是( )A、对称轴为直线 B、当 时, 随 的增大而减小 C、与 轴没有交点 D、与 轴交于点21. 已知一次函数 ( , 为常数, ), ( , 为常数, )的图象如图所示,则函数 的图象可能是( )
A、 B、 C、-4 D、-220. 关于抛物线 ,下列结论中不正确是( )A、对称轴为直线 B、当 时, 随 的增大而减小 C、与 轴没有交点 D、与 轴交于点21. 已知一次函数 ( , 为常数, ), ( , 为常数, )的图象如图所示,则函数 的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 22. 已知点 是一次函数 图象上任意一点,则 的值等于( )A、1 B、-1 C、 D、23. 关于二次函数y=(x-1)2+2,下列说法正确的是( )A、图象与y轴的交点坐标为(0,2) B、图象的对称轴在y轴的左侧 C、y的最大值为2 D、当x>1时,y的值随x值的增大而增大24. 关于 的二次函数 在 的范围内 随 的增大而减小,则 满足的条件是( ).A、 B、 C、 D、25. 在抛物线y=a(x﹣m﹣1)2+c(a≠0)和直线y=﹣ x的图象上有三点(x1 , m)、(x2 , m)、(x3 , m),则x1+x2+x3的结果是( )A、 B、0 C、1 D、226. 函数y=kx﹣2与y= (k≠0)在同一坐标系内的图象可能是( )A、
22. 已知点 是一次函数 图象上任意一点,则 的值等于( )A、1 B、-1 C、 D、23. 关于二次函数y=(x-1)2+2,下列说法正确的是( )A、图象与y轴的交点坐标为(0,2) B、图象的对称轴在y轴的左侧 C、y的最大值为2 D、当x>1时,y的值随x值的增大而增大24. 关于 的二次函数 在 的范围内 随 的增大而减小,则 满足的条件是( ).A、 B、 C、 D、25. 在抛物线y=a(x﹣m﹣1)2+c(a≠0)和直线y=﹣ x的图象上有三点(x1 , m)、(x2 , m)、(x3 , m),则x1+x2+x3的结果是( )A、 B、0 C、1 D、226. 函数y=kx﹣2与y= (k≠0)在同一坐标系内的图象可能是( )A、 B、
B、 C、
C、 D、
D、