湘教版初中数学九年级下册2.7正多边形与圆同步练习

试卷更新日期：2022-02-21 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，已知正五边形 $A B C D E$ 内接于 $⊙ O$ ，连结 $B D$ ，则 $∠ A B D$ 的度数是（）

A、 $60 °$ B、 $70 °$ C、 $72 °$ D、 $144 °$

查看试题解析
2. 如图，正五边形ABCDE内接于⊙O，连接AC，则∠ACD的度数是（）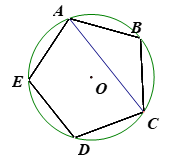

A、72° B、70° C、60° D、45°

查看试题解析
3. 如图，正六边形 $A B C D E F$ 内接于圆O，半径为4，则这个正六边形的边心距 $O M$ 为（）

A、2 B、 $2 \sqrt{3}$ C、 $\sqrt{3}$ D、 $1$

查看试题解析
4. 如图， $⊙ O$ 是正方形 $A B C D$ 的外接圆，若 $⊙ O$ 的半径为4，则正方形 $A B C D$ 的边长为（）

A、4 B、8 C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
5. 阅读图中的材料，解答下面的问题：已知⊙O是一个正十二边形的外接圆，该正十二边形的半径为2，如果用它的面积来近似估计⊙O的面积，则⊙O的面积大约是（）

A、12 B、12.4 C、12.56 D、 $4 π$

查看试题解析
6. 如图，正方形ABCD内接于⊙O，点P在 $\overset{⌢}{A B}$ 上，则∠BPC的度数为（　　）

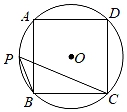A、30° B、45° C、60° D、90°

查看试题解析
7. 如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为6，则阴影部分的面积为（　　）

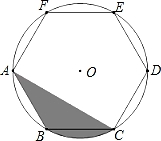A、12π B、6π C、9π D、18π

查看试题解析
8. 圆内接正方形的面积为a，则圆的面积为（）

A、 $\frac{π a}{2}$ B、2πa C、 $\frac{π a^{2}}{2}$ D、πa²

查看试题解析
9. 如图，正六边形 $A B C D E F$ 的边长为6，以顶点A为圆心， $A B$ 的长为半径画圆，则图中阴影部分的面积为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $12 π$

查看试题解析
10. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H（如图）.图中阴影部分的面积记为S，三条线段GB、BC、CH的长度之和记为l，大正六边形在绕点O旋转过程中，下列说法正确的是（）

A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变

查看试题解析
11. 如图，在正五边形ABCDE中，记∠BCD＝x°，∠ACB＝y°，则 $\frac{x}{y}$ 等于（）

A、 $\frac{3}{2}$ B、2 C、3 D、4

查看试题解析
12. 如图，正五边形ABCDE内接于⊙O，连接AC，则∠BAC的度数是（）

A、45° B、38° C、36° D、30°

查看试题解析

二、填空题

13. 如图，∠1是正五边形两条对角线的夹角，则∠1=度.

查看试题解析
14. 斛是中国古代的一种量器.据《汉书 .律历志》记载：“斛底，方而圜（huán）其外，旁有庣（tiāo）焉”．意思是说：“斛的底面为：正方形外接一个圆，此圆外是一个同心圆” . 如图所示，
问题：现有一斛，其底面的外圆直径为两尺五寸（即2.5尺），“庣旁”为两寸五分（即两同心圆的外圆与内圆的半径之差为0.25尺），则此斛底面的正方形的边长为尺．

查看试题解析
15. 若一个正多边形的边长等于它的外接圆的半径，则这个正多边形是正边形．

查看试题解析
16. 如图，边长为1的正六边形 $A B C D E F$ 放置于平面直角坐标系中，边 $A B$ 在x轴正半轴上，顶点F在y轴正半轴上，将正六边形 $A B C D E F$ 绕坐标原点O顺时针旋转，每次旋转 $60 °$ ，那么经过第2022次旋转后，顶点D的坐标为．

查看试题解析
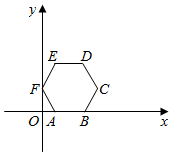17. 边长为a的正六边形中连接不相邻的两个顶点，组成如图所示的内部为六边形的图形.则阴影部分周长等于.

查看试题解析
18. 在正六边形的外接圆中，任一边所对的圆周角的度数为.

查看试题解析
19. 如图，正方形ABCD内接于⊙O，点P在 $\overset{⌢}{A B}$ 上，则∠BPC的度数为.

查看试题解析
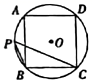20. 如图，五边形ABCDE是 $⊙ O$ 的内接正五边形，则 $∠ O D C$ 的度数是.

查看试题解析
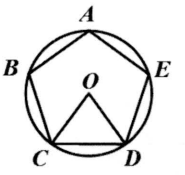21. 如图，A、B、C、D为一个正多边形的顶点，O为正多边形的中心，若∠ADB＝15°，则这个正多边形的边数为．

查看试题解析
22. 如图，已知正六边形ABCDEF的外接圆半径为2cm，则正六边形的边心距是cm.

查看试题解析

三、解答题

23. 已知圆内接正十二边形的面积为S，求同圆的内接正六边形的面积．

查看试题解析
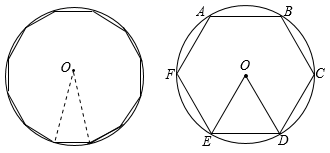24. 图1是由六个全等且边长为2的小正五边形，以及五个全等且顶角为36°、腰长为2的等腰三角形镶嵌而成的一个大正五边形，正五边形和等腰三角形的顶点称为格点，连接格点而成的三角形称为格点三角形.在图2的三个图中，分别画出一个与图中已知△ABC相似但不全等的格点三角形，并注明三角形的顶点字母.

查看试题解析
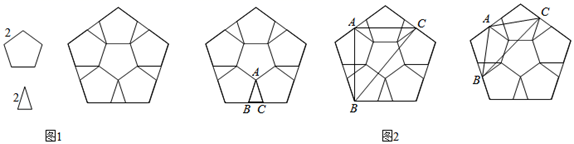25. 试比较图中两个几何图形的异同，请分别写出它们的两个相同点和两个不同点。例如，相同点：正方形的对角线相等，正五边形的。对角线也相等；不同点：正方形是中心对称图形，正五边形不是中心对称图形。

相同点：①；②

不同点：①；②.

查看试题解析

四、综合题

26. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点，且BM＝CN，连接OM、ON

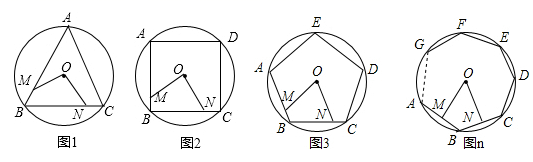(1)、求图1中∠MON的度数

(2)、图2中∠MON的度数是，图3中∠MON的度数是

(3)、试探究∠MON的度数与正n边形边数n的关系是

查看试题解析
27. 如图，在⊙O的内接四边形ABCD中，AB＝AD，∠C＝120°，点E在弧AD上，连接OA、OD、OE、AE、DE.

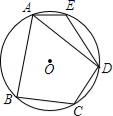(1)、求∠AED的度数；

(2)、当∠DOE＝90°时，AE恰好为⊙O的内接正n边形的一边，求n的值.

查看试题解析
28. 某同学在学习了正多边形和圆之后，对正五边形的边及相关线段进行研究，发现多处出现者名的黄金分割比 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ．如图，圆内接正五边形 $A B C D E$ ，圆心为O， $O A$ 与 $B E$ 交于点H， $A C$ 、 $A D$ 与 $B E$ 分别交于点M、N．根据圆与正五边形的对称性，只对部分图形进行研究．（其它可同理得出）

(1)、求证： $△ A B M$ 是等腰三角形且底角等于36°，并直接说出 $△ B A N$ 的形状；

(2)、求证： $\frac{B M}{B N} = \frac{B N}{B E}$ ，且其比值 $k = \frac{\sqrt{5} - 1}{2}$ ；

(3)、由对称性知 $A O ⊥ B E$ ，由（1）（2）可知 $\frac{M N}{B M}$ 也是一个黄金分割数，据此求 $\sin 18 °$ 的值．

查看试题解析