湘教版初中数学九年级下册2.1圆心角、圆周角同步练习
试卷更新日期：2022-02-18 类型：同步测试
一、单选题
-
1. 如图，中， ， 则等于（ ）
A、 B、 C、 D、2. 如图，已知BC是⊙O的直径，∠AOC＝58°，则∠A的度数为（ ）
A、28° B、29° C、32° D、42°3. 如图，中，弦相交于点 ， 则（ ）.
A、 B、 C、 D、4. 如图，是的直径， ， 则（ ）
A、 B、 C、 D、5. 如图，D是等边△ABC外接圆 上的点，且∠CAD=20°，则∠ACD的度数为（ ）
A、20° B、30° C、40° D、45°6. 如图，点A，B，C都在⊙O上，连接CA，CB，OA，OB.若∠AOB=140°，则∠ACB为（ ）
A、40° B、50° C、70° D、80°7. 如图，菱形ABCD的顶点B，C，D均在⊙A上，点E在弧BD上，则∠BED的度数为（ ）
A、90° B、120° C、135° D、150°8. 如图，四边形ABCD内接于⊙O，若∠ADC＝140°，则∠AOC的度数为（ ）
A、25° B、80° C、130° D、100°9. 如图，四边形内接于 ， 为的直径，.若 ， 则的大小是（ ）
A、55° B、70° C、110° D、140°10. 如图，AB是⊙O的直径，点C，D为⊙O上的点．若∠D＝120°，则∠CAB的度数为（ ）
A、30° B、40° C、50° D、60°11. 如图所示，在⊙O中， ，∠A=30°，则∠B=（ ）
A、150° B、75° C、60° D、15°12. 以下命题：①直径相等的圆是等圆；②长度相等弧是等弧；③相等的弦所对的弧也相等；④圆的对称轴是直径；其中正确的个数是（ ）A、4 B、3 C、2 D、1二、填空题
-
13. 如图，在⊙O的内接四边形ABCD中，∠BCD=130°，则∠BOD的度数是度．
14. 如图，四边形ABCD是半圆O的内接四边形，其中AB是直径，点C是弧DB的中点，若∠C＝110°，则∠ABC的度数= ．
15. 如图，半圆 的直径 ，将半圆 绕点B顺时针旋转45°得到半圆 ，与AB交于点P，那么AP的长为.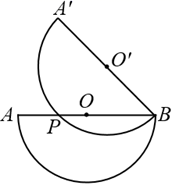
16. 如图，在中，是直径，弦的长为5cm，点D在圆上，且 ， 则的半径为 ．
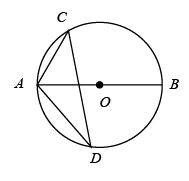17. 如图，量角器外沿上有A、B两点，它们的读数分别是70°、40°，则∠1的度数为度．
18. 如图，点A、B、C是上的点， ， 则的度数为.
19. 如图，AB为⊙O的直径，点P为其半圆上任意一点（不含A、B），点Q为另一半圆上一定点，若∠POA为x°，∠PQB为y°，则y与x的函数关系是.
20. 如图，点A、B、C在⊙O上，BC＝6，∠BAC＝30°，则⊙O的半径为 ．
21. 如图，点A、B把⊙O分成 两条弧，则∠AOB= ．
22. 如图，在⊙O中，C，D分别是OA，OB的中点，MC⊥AB，ND⊥AB，M，N在⊙O上．下列结论：①MC＝ND；② ；③四边形MCDN是正方形；④MN＝ AB，其中正确的结论是(填序号)．
三、解答题
-
23. 如图，是上的四个点，.判断的形状，并证明你的结论.
24. 如图，是的外接圆⊙O的直径，若∠ACB=50°，求∠BAD的度数．
25. 如图，的三个顶点都在⊙O上，直径 ， .求的长.
26. 如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．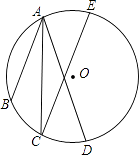
四、综合题
-
27. 如图，已知AB是⊙O的直径，AB=6，sinC＝ ．
(1)、求弦AD的长．(2)、过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．求DF的长．
