江苏省常州市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-02-18 类型:期末考试
一、单选题
-
1. 下列单项式中, 的同类项是( )A、 B、 C、 D、2. 若 和 都是关于 的五次多项式,则 是( )A、关于 的五次多项式 B、关于 的十次多项式 C、关于 的四次多项式 D、关于 的不超过五次的多项式或单项式3. 2021年5月18日上午,江苏省人民政府召开新闻发布会,公布了全省最新人口数据,其中连云港市的常住人口约为4600000人.把“4600000”用科学记数法表示为( )A、 B、 C、 D、4. 已知 ,则代数式 的值是( )A、31 B、 C、41 D、5. 某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )A、先打九五折,再打九五折 B、先提价 ,再打六折 C、先提价 ,再降价 D、先提价 ,再降价6. 下列说法不正确的是( )A、过任意一点可作已知直线的一条平行线 B、在同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、直线外一点与直线上各点连接的所有线段中,垂线段最短7. 如图,将直角三角板放置在矩形纸片上,若 ,则 的度数为( )
 A、42° B、48° C、52° D、60°8. 将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( )
A、42° B、48° C、52° D、60°8. 将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( )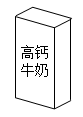 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. .10. 若多项式3xa+3﹣x3﹣a+4是四次三项式,则a=.11. 观察下列等式: , , ,…按此规律,则第 个等式为 .12. 若关于x的方程的解是 , 则a的值为.13. 我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两,银子共有两.(注:明代时1斤=16两)14. 的余角是 .15. 如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=.
 16. 如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面.(填字母)
16. 如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面.(填字母) 17. 拓展探索:有若干个数,第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第 个数记为 ,若 ,从第二个数起,每个数都等于1与它前面那个数的差的倒数,如: ,…如此计算,则 , ;根据你的推断, .18. 有下列说法:①两条直线被第三条直线所截,内错角相等;②过一点有且只有一条直线与已知直线垂直;③在连接直线外一点与直线上各点的线段中,垂线段最短;④在同一平面中,两条直线不相交就平行.其中正确的结论是(填序号).
17. 拓展探索:有若干个数,第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第 个数记为 ,若 ,从第二个数起,每个数都等于1与它前面那个数的差的倒数,如: ,…如此计算,则 , ;根据你的推断, .18. 有下列说法:①两条直线被第三条直线所截,内错角相等;②过一点有且只有一条直线与已知直线垂直;③在连接直线外一点与直线上各点的线段中,垂线段最短;④在同一平面中,两条直线不相交就平行.其中正确的结论是(填序号).三、解答题
-
19.(1)、(2)、20. 某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9(1)、请你替这位同学求出的正确答案;(2)、当x取任意数值,A-3B的值是一个定值,求y的值.21.(1)、﹣3x+7=4x+21;(2)、 ﹣1= +x;22. 如图,方格纸中小正方形的边长均为1cm,三角形ABC的顶点均为格点.
 (1)、过点C画AB的平行线l1;(2)、过点C画AB的垂线l2;(3)、三角形ABC的面积=cm2.23. 如图,已知∠AOC=2∠BOC,与∠AOC相加为90°的角比∠BOC小30°.
(1)、过点C画AB的平行线l1;(2)、过点C画AB的垂线l2;(3)、三角形ABC的面积=cm2.23. 如图,已知∠AOC=2∠BOC,与∠AOC相加为90°的角比∠BOC小30°.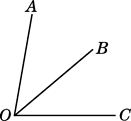 (1)、求∠AOB的度数;(2)、过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.24. 若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 ,-1的差倒数为 ,现已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,…,依此类推.(1)、分别求出 , , 的值;(2)、计算 的值;(3)、计算 的值.25. 如图①是由一些大小相同的小正方体组合成的简单几何体.(1)、请在图 的方格纸中分别画出它的主视图、左视图和俯视图.
(1)、求∠AOB的度数;(2)、过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.24. 若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 ,-1的差倒数为 ,现已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,…,依此类推.(1)、分别求出 , , 的值;(2)、计算 的值;(3)、计算 的值.25. 如图①是由一些大小相同的小正方体组合成的简单几何体.(1)、请在图 的方格纸中分别画出它的主视图、左视图和俯视图.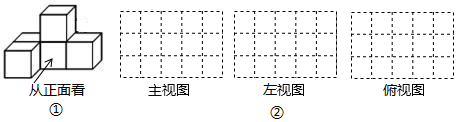 (2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.26. 甲、乙两个工程队第一次合作完成6000米的公路修建工程,两队的修建速度及每天所需工程费的情况如表所示,最终甲队的工作天数比乙队的工作天数的2倍少20天.
(2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.26. 甲、乙两个工程队第一次合作完成6000米的公路修建工程,两队的修建速度及每天所需工程费的情况如表所示,最终甲队的工作天数比乙队的工作天数的2倍少20天.甲
乙
修建速度(米/天)
90
80
每天所需工程费(元)
1200
1000
(1)、甲、乙两队分别工作了多少天?完成该项工程甲、乙两队所需工程费各多少元?(2)、甲、乙两个工程队第二次又合作完成某项公路修建工程,其中乙队分到的工作量是它的第一次的2倍,同时由于乙队减少了人员和设备,修建速度比它的第一次减少了25%,每天所需工程费也因此而打折.完成该项任务后,乙队所需工程费比它的第一次多了38000元,求乙队第二次每天所需工程费是它的第一次的几折?27. 探索新知:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB , ∠AOC和∠BOC , 若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
 (1)、一个角的平分线这个角的“巧分线”;(填“是”或“不是”)(2)、如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=;(用含α的代数式表示出所有可能的结果)(3)、当t为何值时,射线PM是∠QPN的“巧分线”;(4)、若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
(1)、一个角的平分线这个角的“巧分线”;(填“是”或“不是”)(2)、如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=;(用含α的代数式表示出所有可能的结果)(3)、当t为何值时,射线PM是∠QPN的“巧分线”;(4)、若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.