湘教版初中数学八年级下册1.1直角三角形的判定与性质(Ⅰ)同步练习
试卷更新日期:2022-02-18 类型:同步测试
一、单选题
-
1. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴2. 下列命题正确的是( )A、同位角相等 B、相等的圆心角所对的弧相等 C、对角线相等的四边形是矩形 D、直角三角形斜边上的中线等于斜边的一半3. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
 A、5 B、4 C、3 D、24. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )
A、5 B、4 C、3 D、24. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )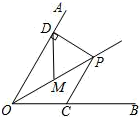 A、 B、 C、 D、5. 如图,Rt△ABC中,∠C=90°,∠B=60°.首先以顶点B为圆心、适当长为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若BG=1,P为边AB上一动点,则GP的最小值为( )
A、 B、 C、 D、5. 如图,Rt△ABC中,∠C=90°,∠B=60°.首先以顶点B为圆心、适当长为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若BG=1,P为边AB上一动点,则GP的最小值为( )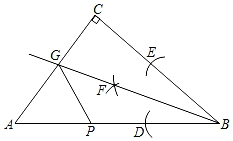 A、无法确定 B、 C、1 D、26. 等腰三角形的底角是 ,腰长为10,则其腰上的高为( )A、8 B、7 C、5 D、47. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD是△ABC的高,且BD=2,则AD的长为( )
A、无法确定 B、 C、1 D、26. 等腰三角形的底角是 ,腰长为10,则其腰上的高为( )A、8 B、7 C、5 D、47. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD是△ABC的高,且BD=2,则AD的长为( ) A、6 B、7 C、8 D、98. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于( )
A、6 B、7 C、8 D、98. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于( )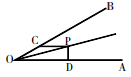 A、3 B、2.5 C、2 D、19. 如图,在四边形ABCD中, , , , ,则 的长为( )
A、3 B、2.5 C、2 D、19. 如图,在四边形ABCD中, , , , ,则 的长为( )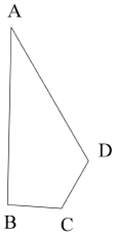 A、2 B、1.5 C、3 D、2.510. 如图如果将一副三角板按如图方式叠放,那么 等于( )
A、2 B、1.5 C、3 D、2.510. 如图如果将一副三角板按如图方式叠放,那么 等于( )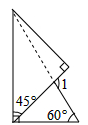 A、 B、 C、 D、11. 如图,在 中,∠ACB=90°,∠A=30°,BC=4,CD是高,则AD的长为( )
A、 B、 C、 D、11. 如图,在 中,∠ACB=90°,∠A=30°,BC=4,CD是高,则AD的长为( )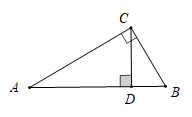 A、5 B、6 C、7 D、812. 下列说法错误的是( )A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、直角三角形斜边上的中线等于斜边的一半 D、对角线互相垂直的四边形是菱形
A、5 B、6 C、7 D、812. 下列说法错误的是( )A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、直角三角形斜边上的中线等于斜边的一半 D、对角线互相垂直的四边形是菱形二、填空题
-
13. 将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式.14. 已知在 Rt△ABC 中,∠C=90°,∠A=37°,则∠B=.15. 若直角三角形斜边上的中线等于3,则这个直角三角形的斜边长为16. (知识衔接)
⑴长方形的对角线相等且互相平分;
⑵直角三角形斜边上的中线等于斜边的一半.
(问题解决)如图,在 中, , 于点 , 为 的中点,连结 , .下列结论:

① ;② ;③S四边形DEBC ;④ .正确的是
17. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .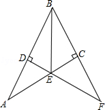 18. 如图,AD平分∠BAC , DE AB , DF⊥AB . 若AE=8,∠BAC=30°,则DF的长为 .
18. 如图,AD平分∠BAC , DE AB , DF⊥AB . 若AE=8,∠BAC=30°,则DF的长为 .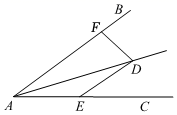 19. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB , 交BC于点D , 若CD=1,则BD= .
19. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB , 交BC于点D , 若CD=1,则BD= .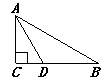 20. 如图,在 中, , , ,交 于点D,且 ,则 .
20. 如图,在 中, , , ,交 于点D,且 ,则 .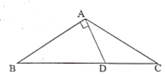 21. 如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是
21. 如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是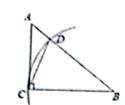 22. 当三角形中的一个内角α是另一个内角β的一半时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为直角三角形,则这个“特征角”的度数为.
22. 当三角形中的一个内角α是另一个内角β的一半时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为直角三角形,则这个“特征角”的度数为.三、解答题
-
23. 如图,AF,AD分别是 的高和角平分线,且 , ,求 的度数.
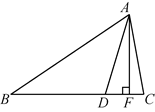 24. 如图,△ABC中,∠C=90°.
24. 如图,△ABC中,∠C=90°.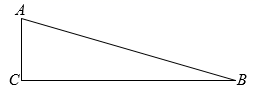 (1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .25. 阅读下列材料,完成相应任务.
(1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .25. 阅读下列材料,完成相应任务.直角三角形斜边上的中线等于斜边的一半
如图1, 中, , 是斜边 上的中线.求证: .
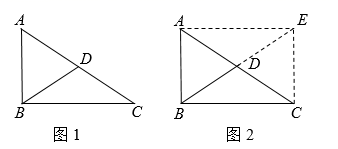
分析:要证明 等于 的一半.可以用“倍长法”将 延长一倍,如图2,延长 到 ,使得 .连接 , .可证四边形 是矩形,由矩形的对角线相等得 ,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到 .
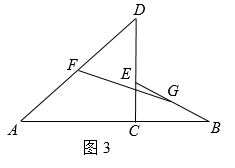 (1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .
(1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .四、综合题
-
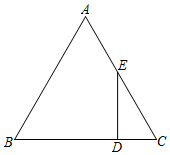
26. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.
 27. 小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
27. 小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题: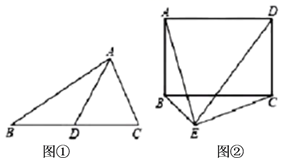 (1)、他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在 中, 是 边上的中线,若 ,求证: .(2)、如图②,已知矩形 ,如果在矩形外存在一点 ,使得 ,求证: .(可以直接用第(1)问的结论)(3)、在第(2)问的条件下,如果 恰好是等边三角形,请求出此时矩形的两条邻边 与 的数量关系.28. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).
(1)、他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在 中, 是 边上的中线,若 ,求证: .(2)、如图②,已知矩形 ,如果在矩形外存在一点 ,使得 ,求证: .(可以直接用第(1)问的结论)(3)、在第(2)问的条件下,如果 恰好是等边三角形,请求出此时矩形的两条邻边 与 的数量关系.28. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).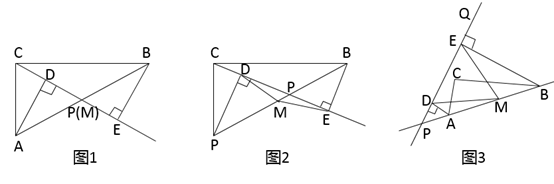 (1)、如图1,当点P与点M重合时,AD与BE的位置关系是 , MD与ME的数量关系是.(2)、如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;(3)、如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.
(1)、如图1,当点P与点M重合时,AD与BE的位置关系是 , MD与ME的数量关系是.(2)、如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;(3)、如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.