湖南省岳阳经济技术开发区2021-2022学年九年级上学期期末考试数学试卷

试卷更新日期：2022-02-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各点中，在反比例函数 $y = \frac{3}{x}$ 图象上的是（）

A、 $(- 3 ， 1)$ B、 $(3 ， 1)$ C、 $(- 3 ， - \frac{1}{3})$ D、 $(\frac{1}{3} ， 3)$

查看试题解析
2. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x - 1)}^{2} = 6$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
3. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $\cos B = \frac{1}{2}$ ，则 $\sin A$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
4. 为了解甲、乙、丙、丁四位选手射击水平，随机让四人各射击10次，计算四人10次射击命中环数平均数都是9.3环，方差（环²）如下表.则这四位选手成绩最稳定的是（）

选手

甲

乙

丙

丁

方差

0.035

0.016

0.022

0.025

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 如图，点F是矩形ABCD的边CD上一点，射线BF交AD的延长线于点E，则下列结论错误的是（）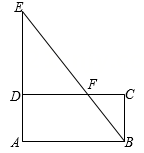

A、 $\frac{E D}{E A} = \frac{E F}{E B}$ B、 $\frac{E D}{B C} = \frac{E F}{B F}$ C、 $\frac{D F}{A B} = \frac{E D}{D A}$ D、 $\frac{B F}{B E} = \frac{C F}{C D}$

查看试题解析
6. 下列命题正确的是（）

A、已知：线段 $a = 1 c m$ ， $b = 2 c m$ ， $c = 3 c m$ ， $d = 4 c m$ ，则a，b，c，d是比例线段 B、已知关于x的方程 $(m^{2} + 1) x^{2} - 3 = 0$ 是一元二次方程 C、已知点 $A (- 1 ， y_{1})$ 、 $B (- 2 ， y_{2})$ 是函数 $y = - \frac{5}{x}$ 图象上的两点，则 $y_{2} > y_{1}$ D、位似图形一定是相似图形，相似图形也一定是位似图形

查看试题解析
7. 关于x的一元二次方程 $x^{2} + 2 x - k^{2} = 0$ 的根的情况是（）

A、没有实数根 B、不一定有实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
8. 如图，在平面直角坐标系中，点A是双曲线 $y_{1} = \frac{k_{1}}{x} (x > 0)$ 的图象上任意一点，连接AO，过点O作AO的垂线与双曲线 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 交于点B，连接AB，且 $\sin B = \frac{\sqrt{5}}{5}$ ，则 $\frac{k_{1}}{k_{2}} =$ （）

A、 $- \frac{\sqrt{5}}{5}$ B、 $- \frac{1}{2}$ C、 $- \frac{1}{4}$ D、 $- \frac{1}{5}$

查看试题解析

二、填空题

9. 已知 $\frac{b}{a} = \frac{3}{5}$ ，那么 $\frac{a - b}{a} =$ .

查看试题解析
10. 随机抽取某城市面积为 $30 k m^{2}$ 的土地调查后，估算出森林覆盖率为40%，若该城市所占面积为 $120 {km}^{2}$ ，据此估算该城市森林覆盖面积为 ${km}^{2}$ .

查看试题解析
11. 若 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ， $\frac{A B}{A^{'} B^{'}} = \frac{3}{4}$ ， $△ A B C$ 的面积为 $3 {cm}^{2}$ ，则 $△ A^{'} B^{'} C^{'}$ 的面积为 ${cm}^{2}$ .

查看试题解析
12. 某防洪大堤的横断面是如图所示的梯形ABCD，坝高 $A H = 3$ 米，背水坡AB的坡度 $i = 1 ： 3$ ，则斜坡AB的长为米.

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - b x + 2 = 0$ 有一个根为1，则方程另一个根为.

查看试题解析
14. 如图，在每个小正方形的边长为1的网格中， $△ A B C$ 的顶点A、B、C均落在格点上，则 $\cos ∠ A B C =$ .

查看试题解析
15. 《九章算术》是我国古代数学的经典著作，它的出现标志着中国古代数学形成了完整的体系，其“勾股”章中记载了一个数学问题：“今有户高多于广六尺，两隅相去适一丈，问户高、广各几何？”译文为：“已知有一扇矩形门的高比宽多6尺，门的对角线长为1丈（1丈＝10尺），那么门的高和宽各是多少？”如果设门的宽为x尺，则可列方程为．

查看试题解析
16. 在平面直角坐标系中，将一点的横坐标与纵坐标互换后得到的点称为它的“互换点”，点M和A为函数 $y = \frac{k}{x} (k > 0)$ 的图象第一象限上的一组互换点（M点在A点的左侧）.直线AM分别交x轴、y轴于C、D两点，连接AO交双曲线另一支于点B，连接BM分别交x轴、y轴于点E，F.则下列结论正确的是.（写出所有正确结论的序号）

① $△ O C A ≅ △ O D M$ ；② $M A = D M + A C$ ；③若 $M F = \frac{2}{7} M B$ ，则 $M D = \frac{2}{3} M A$ ；④若 $∠ M O A = 60 °$ ，M点的横坐标为1，则 $k = \sqrt{3} + 2$

查看试题解析

三、解答题

17.

(1)、计算： $2 \sin 60 ° + \tan 60 °$

(2)、解方程： ${(x - 1)}^{2} - 9 = 0$

查看试题解析
18. 如图，已知 $A B / / D C$ ，点E、F在线段BD上， $A B = 2 D C$ ， $B E = 2 D F$ ，求证： $△ A B E ∽ △ C D F$

查看试题解析
19. 如图，已知函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = 2 x + 2$ 的图象交于点 $A (m ， 4)$ 和点B.

(1)、求反比例函数的关系式；

(2)、如果点C与点A关于x轴对称，求 $△ A B C$ 的面积.

查看试题解析
20. 为满足春节市场需求，某商场在节前购进大批某品牌童装，该品牌童装若每件盈利40元，平均每天可售出20件，经调查发现，若每件童装降价1元，商场平均每天可多售出2件，若商场希望该品牌童装日盈利为1200元，同时为了尽量减少库存，请问该童装应降价多少元最合适？

查看试题解析
21. 为深入开展青少年毒品预防教育工作，增强学生禁毒意识，某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动，并随机抽查了部分同学的成绩，整理并制作成图表如下：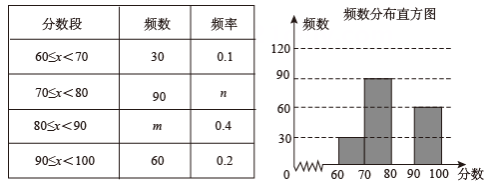

根据以上图表提供的信息，回答下列问题：

(1)、抽查的人数为人， $n =$ ；

(2)、请补全频数分布直方图；

(3)、若成绩在80分以上（包括80分）为“优秀”，请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名？

查看试题解析
22. 随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场 $B ， C$ 两点之间的距离.如图所示，小星站在广场的 $B$ 处遥控无人机，无人机在 $A$ 处距离地面的飞行高度是 $41 .6m$ ，此时从无人机测得广场 $C$ 处的俯角为 $63 °$ ，他抬头仰视无人机时，仰角为 $α$ ，若小星的身高 $B E = 1.6 m ， E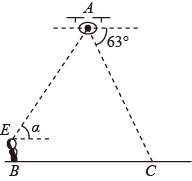 A = 50 m$ （点 $A ， E ， B ， C$ 在同一平面内）.

(1)、求仰角 $α$ 的正弦值；

(2)、求 $B ， C$ 两点之间的距离（结果精确到 $1m$ ）.
$(\sin 63 ° \approx 0.89 ， \cos 63 ° \approx 0.45 ， \tan 63 ° \approx 1.96 ， \sin 27 ° \approx 0.45 ， \cos 27 ° \approx 0.89 ， \tan 27 ° \approx 0.51)$

查看试题解析
23. 在 $△ A O B$ 和 $△ C O D$ 中， $∠ A O B = ∠ C O D = 90 °$ ，连接BD，AC，直线BD交AC于点E，交OA于点F.

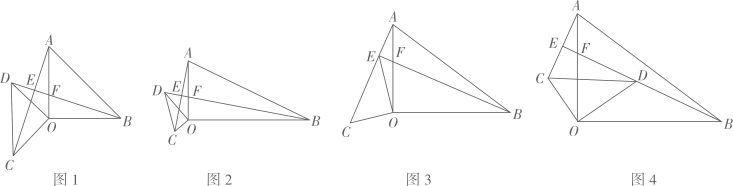(1)、特例发现：如图1，若 $O A = O B$ ， $O C = O D$ .推断：
① $\frac{B D}{A C} =$ ；② $∠ B E C$ 的度数为.

(2)、探究证明：如图2，若 $\frac{O B}{O A} = \frac{O D}{O C} = k$ .判断 $\frac{B D}{A C}$ 的值及 $∠ B E C$ 的度数，并说明理由.

(3)、拓展延伸：在（2）的条件下：若 $O A = 6$ ， $O B = 8$ ，
①将 $△ O C D$ 绕点O顺时针旋转，使点D与点E第一次重合，如图3，此时 $\sin ∠ O A C = \frac{2}{5}$ ，求OC的长；

②在点D与点E第一次重合后，若将①重得到的 $△ O C D$ 继续顺时针旋转，当点D在 $△ A O B$ 内部时，如图4，线段BE的长度是否存在最大值？若存在，请直接写出最大值；若不存在，请说明理由.

查看试题解析
24. $R t △ A B C$ 在直角坐标系内的位置如图所示，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限内的图象与BC边交于点 $D (4 ， m)$ ，与AB交于点 $E (2 ， n)$

(1)、求m与n的数量关系.

(2)、当 $\tan ∠ B A C = \frac{1}{2}$ 时，记 $△ B D E$ 面积为S，用含有k的式子表示S.

(3)、若 $△ B D E$ 的面积为2.设P是线段AB边上的点，在（2）的条件下，是否存在点P，以B，C，P为顶点的三角形与 $△ E D B$ 相似？若存在，求出此时点P的坐标；若不存在，请说明理由.

查看试题解析

选手	甲	乙	丙	丁
方差	0.035	0.016	0.022	0.025