浙江省台州市临海市2021年中考模拟训练题数学试卷（二）

试卷更新日期：2022-02-18 类型：中考模拟

进入出卷网下载

一、单选题

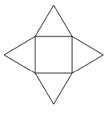
1. 数轴上表示－3的点到原点的距离是（）

A、－3 B、3 C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 如图是某几何体的展开图，则该几何体是（）

A、四棱锥 B、三棱锥 C、四棱柱 D、长方体

查看试题解析
3. 若二次根式 $\sqrt{x - 5}$ 有意义，则x的取值范围是（）

A、x＜5 B、x＞5 C、x≤5 D、x≥5

查看试题解析
4. 下列运算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a^{3} \cdot a^{3} = a^{9}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(a^{3})}^{3} = a^{9}$

查看试题解析
5. 平面直角坐标系中，把点A(－3，2)向右平移2个单位，所得点的坐标是（）

A、（－3，0） B、（－3，4） C、（－5，2） D、（－1，2）

查看试题解析
6. 九年级某班有45人，中考体能测试后，体育委员小亮对测试成绩进行了统计分析，为了解哪一个分值的人数最多，应选择下列哪一个统计量（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 今年父亲的年龄是儿子年龄的3倍，5年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁，则下列式子正确的是（）

A、4x－5=3(x－5) B、4x+5=3(x+5) C、3x+5=4(x+5) D、3x－5=4(x－5)

查看试题解析
8. 如图，锐角△ABC中，点D是边AB的中点，点E在边AC上，有如下两个命题：①如果DE//BC，那么DE＝ $\frac{1}{2}$ BC；②如果DE＝ $\frac{1}{2}$ BC，那么DE//BC.下列判断正确的是（）

A、①是真命题，②是假命题 B、①是假命题，②是真命题 C、①②都是真命题 D、①②都是假命题

查看试题解析
9. 如图，正方形ABCD的顶点A、B在⊙O上，顶点C、D在⊙O内，将正方形ABCD绕点B顺时针旋转α度，使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等，则旋转角度α等于（）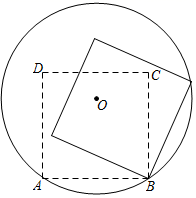

A、36° B、30° C、25° D、22.5°

查看试题解析
10. 如图，这是一张从某大桥正侧面拍摄的照片，大桥的主桥拱为圆弧型，桥面AB长为80米，且与水面平行，小王用计算机根据照片对大桥进行了模拟分析，在桥正下方的水面上取一点P，在桥面AB上取点C，作射线PC交弧（主桥拱）于点D，画出了PC与PD关于AC长的函数图象，下列对此桥的判断不合理的是（）

A、在桥拱正下方部分的桥面EF的实际长度约为50米. B、桥拱的最高点与桥面AB的实际距离约为18米. C、拍摄照片时，桥面离水面的实际高度约为11米. D、桥面上BF段的实际长度约20米.

查看试题解析

二、填空题

11. 比较大小：4 $\sqrt{10}$ .（填“ $>$ ”，“ $<$ ”、“ $=$ ”）

查看试题解析
12. 如图，PB与⊙O相切于点B，OP与⊙O相交于点A，若⊙O的半径为2，∠P＝30°，则 $\overset{⌢}{A B}$ 的长为.

查看试题解析
13. 已知反比例函数 $y = \frac{6}{x}$ ，若x≥2，则y的取值范围为.

查看试题解析
14. 小杰和小丽参加社会实践活动，随机选择“做社区志愿者”和“参加社会调查”两项中的一项，那么两人同时选择“做社区志愿者”的概率是．

查看试题解析
15. 小丽在解一个三次方程x³－2x＋1＝0时，发现有如下提示：观察方程可以发现有一个根为1，所以原方程可以转化为(x－1)(x²＋bx＋c)＝0.根据这个提示，请你写出这个方程的所有的解.

查看试题解析
16. 如图，把一张矩形纸片ABCD沿EF，MN对折，得到五边形GEFNM.其中，顶点A与D重合于点G，重叠部分GHIJ为正方形，顶点I在EM上，若FN=8cm，EM=10cm，则BC长为cm.

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{3})}^{- 1} - (5 - \sqrt{12})$ .

查看试题解析
18. 化简： $(\frac{2}{x - 3} + 1) \cdot \frac{x^{2} - 9}{x - 1}$ .

查看试题解析
19. 如图，某商场从一层到二层的楼梯由台阶AB，CD和一段水平平台BC构成，AB与CD互相平行并且与地面成31°角.已知台阶AB＝5.2米，CD＝2.8米，平台BC＝2.5米.求商场一层的高度（结果精确到0.1米）.参考数据：sin31°≈0.515，cos31°≈0.857，tan31°≈0.601.

查看试题解析
20. 有一个容量为8GB（1GB＝1024MB）的U盘，U盘中已经存储了1个视频文件，其余空间都用来存储照片.若每张照片占用的内存容量均相同，照片数量x（张）和剩余可用空间y（MB）的部分关系如表：

照片数量

100

150

200

400

800

剩余可用空间

5600

5400

5200

4400

2800

(1)、求出y与x之间的关系式.

(2)、若U盘中已经存入1100张照片，那么最多还能存入多少张照片？

查看试题解析
21. 某市一中学组织学生参加防范电信网络诈骗知识竞赛活动.为了解活动的效果，学校从全校900名学生中随机抽取部分学生进行知识测试（测试满分100分，得分x均为不小于60的整数），并将测试成绩分为四个等级：基本合格（60≤x＜70），合格（70≤x＜80），良好（80≤x＜90），优秀（90≤x≤100），制作了如图统计图（部分信息未给出）.

由图中给出的信息解答下列问题：

(1)、求测试成绩为合格的学生人数，并补全频数直方图；

(2)、这次测试成绩的中位数是什么等级？

(3)、已知该市共有15000名中学生参加了这次防范电信网络诈骗知识竞赛，请你根据该学校的成绩估计该市在这次测试中成绩为优秀的人数；

(4)、小王查了该市教育网站发现，全市参加本次测试的15000名学生中，成绩为优秀的有4000人，请你用所学统计知识简要说明实际优秀人数与估计优秀人数出现较大偏差的原因，并对该校在防范电信网络诈骗方面的教育给出简要的评价或建议.

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，点D为AB边的中点，以CD为直径作⊙O，分别与AC，BC，AB交于点E，F，G.

(1)、求证：AE＝CE；

(2)、若CE＝4，CF＝3，求DG的长.

查看试题解析
23. 已知，二次函数y＝ax²＋2ax＋1(a≠0)

(1)、当a为何值时，该函数图象的顶点在x轴上，并写出顶点的坐标；

(2)、已知点( $- 3 ， - \frac{1}{2}$ )，(1，0)，(2，－3)，该函数图象过其中的两点，求此函数的解析式；

(3)、已知a＞0，若点A（b，m)，B(b＋3，n)是该函数图象上的两点，且m＞n，求b的取值范围.

查看试题解析
24. 定义：如图1，四边形EFGH的四个顶点分别在▱ABCD四条边上（不与▱ABCD的顶点重合），我们称四边形EFGH为▱ABCD的内接四边形.

(1)、如图1，若 $▱$ ABCD的内接四边形EFGH是平行四边形，求证：AE＝CG

(2)、若 $▱$ ABCD的内接四边形EFGH是矩形.
①请用无刻度的直尺与圆规，在图2中作出一个符合要求的矩形EFGH.（不必说明作图过程，但要保留作图痕迹）

②如图3，已知 $\sin A = \frac{4}{5}$ ，AB＝10，H是AD的中点，HG＝2HE，求AD的长.

(3)、已知， $▱$ ABCD的内接四边形EFGH是平行四边形，且 $S_{▱ E F G H} = \frac{1}{2} S_{▱ A B C D}$ ，求证：点E，F，G，H中至少存在两个点是▱ABCD边的中点.

查看试题解析

照片数量	100	150	200	400	800
剩余可用空间	5600	5400	5200	4400	2800