浙江省杭州市十三中教育集团2021年九年级下学期中考数学二模试卷

试卷更新日期：2022-02-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 2021的倒数是（）

A、 $\frac{1}{2021}$ B、﹣ $\frac{1}{2021}$ C、﹣2021 D、2021

查看试题解析
2. 如图，直线 $l_{1} / / l_{2}$ ，它们之间的距离是（）

A、线段 $P A$ 的长度 B、线段 $P B$ 的长度 C、线段 $P C$ 的长 D、线段 $P D$ 的长度

查看试题解析
3. 将抛物线y＝2x²向下平移3个单位长度所得到的抛物线是（）

A、y＝2x²+3 B、y＝2x²﹣3 C、y＝2（x﹣3）² D、y＝2（x+3）²

查看试题解析
4. 下面用数学家名字命名的图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 实数 $a ， b$ 在数轴上的对应点的位置如图所示，下列关系式不成立的是（）

A、 $a - 5 > b - 5$ B、 $6 a > 6 b$ C、 $- a > - b$ D、 $a - b > 0$

查看试题解析
6. 如图，△ABC内接于⊙O ，若∠A＝45°，OC＝2，则BC的长为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
7. 如果 $a^{2} - a - 2 = 0$ ，那么代数式 ${(a - 1)}^{2} + (a + 2) (a - 2)$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 小明从 $A$ 处出发沿北偏东50°方向行走至 $B$ 处，又从 $B$ 处沿南偏东70°方向行走至 $C$ 处，则 $∠ A B C$ 等于（）

A、130° B、120° C、110° D、100°

查看试题解析
9. 在平面直角坐标系 $x O y$ 中，对于点 $P (a ， b)$ ，若 $a b > 0$ ，则称点 $P$ 为“同号点”.下列函数的图象不存在“同号点”的是（）

A、 $y = - x + 1$ B、 $y = x^{2} - 2 x$ C、 $y = - \frac{2}{x}$ D、 $y = x + \frac{1}{x}$

查看试题解析
10. 如图，已知 $△ A B C$ 中， $∠ B = 90 °$ ， $D$ ， $E$ 分别为 $B C$ ， $A C$ 的中点，连结 $D E$ ，过 $D$ 作 $A C$ 的平行线与 $∠ C A B$ 的角平分线交于点 $F$ ，连结 $E F$ ，若 $E F ⊥ D F$ ， $A C = 2$ ，则 $∠ D E F$ 的正弦值为（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{4}$ C、 $\frac{\sqrt{5} - 1}{4}$ D、 $\frac{3 + \sqrt{5}}{4}$

查看试题解析

二、填空题

11. 因式分解： $a^{3} - a =$ ．

查看试题解析
12. 如图，在△ABC中，D、E分别为AB、AC边的中点，若DE=2，则BC边的长为．

查看试题解析
13. 已知一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 的平均数是3，则数据 $3 x_{1} - 2$ ， $3 x_{2} - 2$ ， $3 x_{3} - 2$ ， $3 x_{4} - 2$ 的平均数是.

查看试题解析
14. 我国古代数学著作《孙子算经》中记载了这样一个有趣的数学问题“今有五等诸侯，共分橘子 $60$ 颗，人别加三颗，问五人各得几何？”题目大意是：诸侯五人，共同分 $60$ 个橘子，若后面的每个人总比他前一个人多分 $3$ 个，问每个人各分得多少个橘子？若设中间的那个人分得 $x$ 个橘子，依题意可列方程为．

查看试题解析
15. 一颗珍贵的百年老树倾斜程度越来越厉害了.出于对它的保护，需要测量它的高度，做法如下：在地面上选取一点 $C$ ，测得 $∠ B C A = 37 °$ ， $A C = 28$ 米， $∠ B A C = 45 °$ ，则这棵树的高 $A B$ 约为米.（结果精确到0.1，参考数据： $\sin 37 ° \approx 0.6$ ， $\tan 37 ° \approx 0.75$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
16. 如图，点 $C$ 为半圆的中点， $A B$ 是直径，点 $D$ 是半圆上一点， $A C$ 、 $B D$ 交于点 $E$ ，若 $A D = 1$ ， $B D = 7$ ，则 $A C =$ .

查看试题解析

三、解答题

17. 如图，在 $5 \times 6$ 的方格纸中， $△ A B C$ 的顶点均在格点上，仅用无刻度的直尺按要求画图.

(1)、在图 $1$ 中画一个以 $A$ ， $B$ ， $C$ ， $D$ 为顶点的平行四边形，且 $D$ 为格点；

(2)、在图 $2$ 中作直线 $C E ⊥ A B$ （ $E$ 为格点）；

(3)、在图 $3$ 中作 $∠ F B A = ∠ C B A$ （ $F$ 为格点，且不在直线 $B C$ 上）.

查看试题解析
18. 一次函数 $y = a x - a + 1$ （ $a$ 为常数，且 $a < 0$ ）.

(1)、若点 $(2 ， - 3)$ 在一次函数 $y = a x - a + 1$ 的图象上，求 $a$ 的值；

(2)、当 $- 1 \leq x \leq 2$ 时，函数有最大值2，求 $a$ 的值.

查看试题解析
19. 如图，在菱形 $A B C D$ ， $B E ⊥ C D$ 于点 $E$ ， $D F ⊥ B C$ 于点 $F$ .

(1)、求证： $B E = D F$ ；

(2)、若 $∠ A = 45 °$ ，求 $\frac{D E}{C E}$ 的值.

查看试题解析
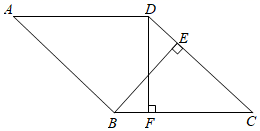20. 某中学开设足球、篮球、乒乓球、羽毛球、排球五项球类活动.为了解学生对这五项活动的喜爱情况，随机调查了 $m$ 名学生（每名学生必选且只能选择这五项活动中的一项），并根据调查结果绘制了如图所示的两幅不完整的统计图.根据统计图提供的信息，解答下列问题：

(1)、 $m =$ ▲ ， ▲ ，并补全条形统计图；

(2)、若全校共有2000名学生，求该校约有多少名学生喜爱乒乓球；

(3)、在抽查的 $m$ 名学生中，学校打算从喜欢羽毛球运动的甲、乙、丙、丁四人中，选取2名参加区中学生羽毛球比赛，请用列表法或画树状图法求同时选中甲、乙的概率.

查看试题解析
21. 如图， $△ O A B$ 中， $O A = O B$ ， $⊙ O$ 过 $A B$ 中点 $C$ ，且与 $O A$ 、 $O B$ 分别交于点 $E$ 、 $F$ .

(1)、求证：直线 $A B$ 是 $⊙ O$ 的切线；

(2)、延长 $A O$ 交 $⊙ O$ 于点 $D$ ，连结 $D F$ 、 $D C$ ，求证： $∠ E D C = ∠ F D C$ ；

(3)、在（2）的条件下，若 $D E = 10$ ， $D F = 6$ ，求 $C D$ 的长.

查看试题解析
22. 已知二次函数 $y = a x^{2} + (1 - a) x + \frac{a}{4}$ .

(1)、若二次函数图象的对称轴为直线 $x = 1$ ，求 $a$ 的值；

(2)、当 $x \geq 2$ 时， $y$ 随 $x$ 的增大而减小，求 $a$ 的取值范围；

(3)、已知 $A (- 1 ， 0)$ ， $B (2 ， 0)$ ，若二次函数的图象与线段 $A B$ 只有一个交点，求 $a$ 的取值范围.

查看试题解析
23. 如图，正方形ABCD中，点E在边AB上运动（不与点A ，B重合），连结EC ，过点E 作EF⊥EC，EF=EC ，过点 F作FP⊥AB，P为垂足，连结CF ，与AD相交于点G .

(1)、求证： $P F = B E$ ；

(2)、当 $E$ 是 $A B$ 的中点时，求 $\frac{A G}{D G}$ 的值；

(3)、设 $x = \frac{A E}{E B}$ ， $y = \frac{A G}{G D}$ ，求 $y$ 关于 $x$ 的函数关系式.

查看试题解析