2021-2022学年度第二学期人教版七年级数学第五章《有理数》5.1相交线课堂练习卷
试卷更新日期：2022-02-18 类型：同步测试
一、单选题
-
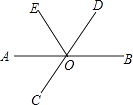
1. 下列语句中，正确的是（ ）A、相等的角一定是对顶角 B、垂线最短 C、过一点有且只有一条直线与已知直线垂直 D、有一个公共顶点，且两边互为反向延长线的两个角是对顶角2. 如图，直线AB，CD相交于点O，OA平分∠EOC，若∠BOD=35°，则∠AOE的度数是（ ）
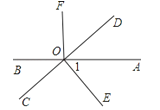
A、70° B、55° C、40° D、35°3.如图，AB，CD相交于点O，OE是∠AOC的平分线，∠BOC=130°，∠BOF=140°，则∠EOF的度数为（ ）
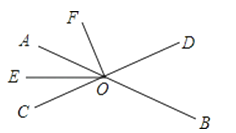A、95° B、65° C、50° D、40°4.如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=110°，则∠BOD的度数是（ ）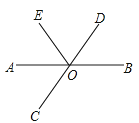
A、25° B、35° C、45° D、55°5. 如图，点A是直线l外一点，过点A作AB⊥l于点B．在直线l上取一点C，连结AC，使AC＝AB，点P在线段BC上，连结AP．若AB＝3，则线段AP的长不可能是（ ）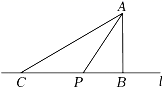
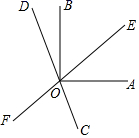
A、3.5 B、4 C、5 D、5.56. 如图．直线l1∥l2 ． AB⊥CD．∠1=34°，那么∠2的度数是（ ）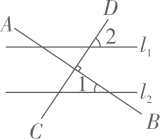
A、34° B、56° C、46° D、44°7. 如图所示，把教室中墙壁的棱看作直线的一部分，那么下列表示两条棱所在的直线的位置关系中不正确的是（ ）
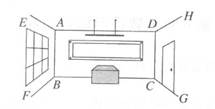A、AB⊥BC B、AD∥BC C、CD∥BF D、AE∥BF8. 以下命题中，真命题的是 （ ）A、两条线只有一个交点 B、同位角相等 C、两边和一角对应相等的两个三角形全等 D、等腰三角形底边中点到两腰的距离相等9. 下列说法中，正确的个数有 （ ）
（1）两条直线被第三条直线所截，内错角相等；（2）对顶角相等；（3）同一平面内，两条直线的位置关系有：相交，垂直和平行三种；（4）同一平面内，不相交的两条直线一定平行.A、2个 B、3个 C、4个 D、1个10. 下列说法中①不相交的两条直线叫做平行线；②对顶角的角平分线在同一直线上；③过一点有且只有一条直线与已知直线平行；④几个有理数相乘，积的符号有负因数的个数确定．正确的个数有 ( )A、1个 B、2个 C、3个 D、4个二、填空题
-
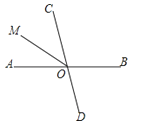
11.
如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠AOC=76°，则∠BOM= °．
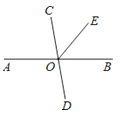
12.如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB=50°，则∠BOD的度数是
13. 如图，已知直线和相交于点 ， 射线在内部， ， 平分 ， 若 ， 则度.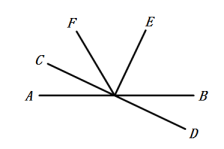
14. 如图，运动会上，小明自踏板M处跳到沙坑P处，甲、乙、丙三名同学分别测得PM＝3.25米，PN＝3.15米，PF＝3.21米，则小明的成绩为 米．（填具体数值）
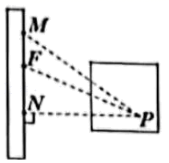15. 某工程队计划把河水引到水池A中，为了节约人力、物力和财力，他们先过A点作 ， 垂足为B，然后沿开渠，这样做的数学依据是 ．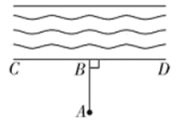
三、解答题
-
16.
已知 与 互为补角， 是 的角平分线，射线 在 内，且 ， ，求 的度数．
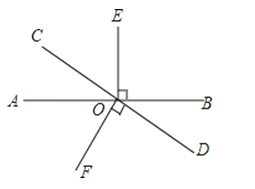
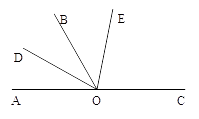17.如图，直线AB，CD相交于点O，OE⊥AB，OF⊥CD．
（1）若OC恰好是∠AOE的平分线，则OA是∠COF的平分线吗？请说明理由；
（2）若∠EOF=5∠BOD，求∠COE的度数．
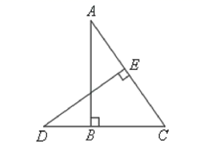
18. 如图，已知AC⊥AE，BD⊥BF，∠1=35°，∠2=35°．AC与BD平行吗？ AE与BF平行吗？根据下面的解答过程填空或填写理由．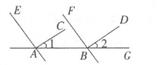
解：∵∠1=35°，∠2= 35°，
∴∠1=∠2（ ），
∴（ ） ∥（ ）（ ）．
又∵AC⊥AE，
∴∠EAC= 90°，
∴∠EAB=∠EAC+∠1=（ ） （ ）
同理可得∠FBD+∠2=（ ），
∴∠EAB=（ ）
∴（ ）∥（ ）（ ）
19. 如图，直线 ， 相交于点 ， ，且 平分 .若 ，求 ， 的度数；
