天津市红桥区2021-2022学年九年级上学期数学期末试卷
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 下列图形中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,属于不可能事件的是( )A、经过红绿灯路口,遇到绿灯 B、射击运动员射击一次,命中靶心 C、班里的两名同学,他们的生日是同一天 D、从一个只装有白球和红球的袋中摸球,摸出黄球3. 下表记录了一名球员在罚球线上投篮的结果:
2. 下列事件中,属于不可能事件的是( )A、经过红绿灯路口,遇到绿灯 B、射击运动员射击一次,命中靶心 C、班里的两名同学,他们的生日是同一天 D、从一个只装有白球和红球的袋中摸球,摸出黄球3. 下表记录了一名球员在罚球线上投篮的结果:投篮次数
50
100
150
200
250
400
500
800
投中次数
28
63
87
122
148
242
301
480
投中频率
0.560
0.630
0.580
0.610
0.592
0.605
0.602
0.600
根据频率的稳定性,估计这名球员投篮一次投中的概率约是( )
A、0.560 B、0.580 C、0.600 D、0.6204. 若是关于x的一元二次方程的一个根,则m的值为( )A、-1 B、0 C、 D、15. 方程的两个根为( )A、 B、 C、 D、6. 某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )A、48(1﹣x)2=36 B、48(1+x)2=36 C、36(1﹣x)2=48 D、36(1+x)2=487. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )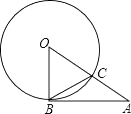 A、40° B、50° C、65° D、75°8. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )A、6,3 B、3 , 3 C、6,3 D、6 , 39. 若一元二次方程的较小根为 , 则下面对的值估计正确的是( )A、 B、 C、 D、10. 如图,在中,以边的中点D为圆心,长为半径画弧,交于E点,若 , 则扇形的面积为( )
A、40° B、50° C、65° D、75°8. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )A、6,3 B、3 , 3 C、6,3 D、6 , 39. 若一元二次方程的较小根为 , 则下面对的值估计正确的是( )A、 B、 C、 D、10. 如图,在中,以边的中点D为圆心,长为半径画弧,交于E点,若 , 则扇形的面积为( ) A、 B、 C、 D、11. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A、 B、 C、 D、11. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )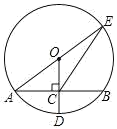 A、2 B、8 C、2 D、212. 已知两点均在抛物线上,点是该抛物线的顶点.若 , 则的取值范围是( )A、 B、 C、 D、
A、2 B、8 C、2 D、212. 已知两点均在抛物线上,点是该抛物线的顶点.若 , 则的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 不透明袋子中装有5个球,其中有2个红球、3个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黑球的概率是 .14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.15. 如图,将矩形绕点A顺时针旋转到矩形的位置,旋转角为 . 若 , 则的大小为(度).
 16. 当时,二次函数的函数值y随自变量x的增大而减小,则m的取值范围是 .17. 汽车刹车后行驶的距离 (单位: )关于行驶的时间 (单位: )的函数解析式是 .汽车刹车后到停下来前进了 .
16. 当时,二次函数的函数值y随自变量x的增大而减小,则m的取值范围是 .17. 汽车刹车后行驶的距离 (单位: )关于行驶的时间 (单位: )的函数解析式是 .汽车刹车后到停下来前进了 .三、解答题
-
18. 如图,在中, .
 (1)、边的长等于 .(2)、用无刻度直尺和圆规,在如图所示的矩形方框内,作出圆心在斜边上,经过点B,且与边相切的 , 并简要说明作法(保留作图痕迹,不要求证明)19. 从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为 . 将这四张扑克牌背面朝上,洗匀.(1)、从中随机抽取一张,则抽取的这张牌的牌面数字能被3整除的概率是;(2)、从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.
(1)、边的长等于 .(2)、用无刻度直尺和圆规,在如图所示的矩形方框内,作出圆心在斜边上,经过点B,且与边相切的 , 并简要说明作法(保留作图痕迹,不要求证明)19. 从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为 . 将这四张扑克牌背面朝上,洗匀.(1)、从中随机抽取一张,则抽取的这张牌的牌面数字能被3整除的概率是;(2)、从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.①利用画树状图或列表的方法,写出取出的两张牌的牌面数字所有可能的结果;
②求抽取的这两张牌的牌面数字之和是偶数的概率.
20. 解下列关于x的方程.(1)、;(2)、 .21. 如图,已知为的直径,切于点C,交的延长线于点D,且 . (1)、求的大小;(2)、若 , 求的长.22. 已知抛物线(为常数)的顶点为 .(1)、求该抛物线的解析式;(2)、点在该抛物线上,当时,比较与的大小;(3)、为该抛物线上一点,当取得最小值时,求点Q的坐标.23. 已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
(1)、求的大小;(2)、若 , 求的长.22. 已知抛物线(为常数)的顶点为 .(1)、求该抛物线的解析式;(2)、点在该抛物线上,当时,比较与的大小;(3)、为该抛物线上一点,当取得最小值时,求点Q的坐标.23. 已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
(Ⅰ)如图①,若∠BAC=25°,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
