上海市静安区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 下列实数中,有理数是( )A、 B、 C、 D、2. 计算的结果是( )A、 B、 C、 D、3. 已知点D、E分别在的边AB、AC的反向延长线上,且ED∥BC,如果AD:DB=1:4,ED=2,那么BC的长是( )A、8 B、10 C、6 D、44. 将抛物线向左平移1个单位,再向上平移1个单位后,所得抛物线的顶点坐标是( )A、 B、 C、(1,0) D、(0,0)5. 如果锐角A的度数是25°,那么下列结论中正确的是( )A、 B、 C、 D、6. 下列说法不正确的是( )A、任意一个直角三角形都可以被分割成两个等腰三角形 B、任意一个等腰三角形都可以被分割成两个等腰三角形 C、任意一个直角三角形都可以被分割成两个直角三角形 D、任意一个等腰三角形都可以被分割成两个直角三角形
二、填空题
-
7. -5的绝对值是 .8. 如果在实数范围内有意义,那么实数的取值范围是9. 已知 , 那么的值是10. 已知线段AB=2cm,点P是AB的黄金分割点,且AP>PB,那么AP的长度是cm(结果保留根号)11. 如果某抛物线开口方向与抛物线的开口方向相同,那么该抛物线有最点(填“高”或“低”)12. 已知反比例函数的图像上的三点 , 判断的大小关系:(用“<”连接)13. 如果抛物线的顶点在轴上,那么常数m的值是14. 如果在A点处观察B点的仰角为 , 那么在B点处观察A点的俯角为(用含的式子表示)15. 如图,在中,AB=AC=6,BC=4,点D在边AC上,BD=BC,那么AD的长是
 16. 在中,DE∥BC,DE交边AB、AC分别于点D、E,如果与四边形BCED的面积相等,那么AD:DB的值为17. 如图,在中,中线AD、BE相交于点G,如果 , 那么(用含向量的式子表示)
16. 在中,DE∥BC,DE交边AB、AC分别于点D、E,如果与四边形BCED的面积相等,那么AD:DB的值为17. 如图,在中,中线AD、BE相交于点G,如果 , 那么(用含向量的式子表示) 18. 如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为
18. 如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为
三、解答题
-
19. 计算:20. 如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高, , , 求AB、CH的长.
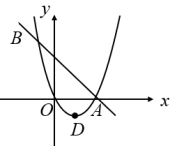
 21. 我们将平面直角坐标系中的图形D和点P给出如下定义:如果将图形D绕点P顺时针旋转90°得到图形 , 那么图形称为图形D关于点P的“垂直图形”.已知点A的坐标为 , 点B的坐标为(0,1),关于原点O的“垂直图形”记为 , 点A、B的对应点分别为点 .
21. 我们将平面直角坐标系中的图形D和点P给出如下定义:如果将图形D绕点P顺时针旋转90°得到图形 , 那么图形称为图形D关于点P的“垂直图形”.已知点A的坐标为 , 点B的坐标为(0,1),关于原点O的“垂直图形”记为 , 点A、B的对应点分别为点 . (1)、请写出:点的坐标为;点的坐标为;(2)、请求出经过点A、B、的二次函数解析式;(3)、请直接写出经过点A、B、的抛物线的表达式为 .22. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字)
(1)、请写出:点的坐标为;点的坐标为;(2)、请求出经过点A、B、的二次函数解析式;(3)、请直接写出经过点A、B、的抛物线的表达式为 .22. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字) 23. 如图,边长为1的正方形ABCD中,对角线AC、BD相交于点O,点Q、R分别在边AD、DC上,BR交线段OC于点P, , QP交BD于点E.
23. 如图,边长为1的正方形ABCD中,对角线AC、BD相交于点O,点Q、R分别在边AD、DC上,BR交线段OC于点P, , QP交BD于点E. (1)、求证:;(2)、当∠QED等于60°时,求的值.
(1)、求证:;(2)、当∠QED等于60°时,求的值.