上海市崇明区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若将抛物线 $y = 2 x^{2}$ 向上平移3个单位，所得抛物线的解析式为（）

A、 $y = 2 x^{2} + 3$ B、 $y = 2 x^{2} - 3$ C、 $y = 2 (x - 3)^{2}$ D、 $y = 2 (x + 3)^{2}$

查看试题解析
2. 如果两个相似三角形的周长比为1：4，那么这两个三角形的对应中线的比为（）

A、1：2 B、1：4 C、1：8 D、1：16

查看试题解析
3. 如果向量 $\overset{⇀}{a}$ 与向量 $\overset{⇀}{b}$ 方向相反，且 $3 | \overset{⇀}{a} | = | \overset{⇀}{b} |$ ，那么向量 $\overset{⇀}{a}$ 用向量 $\overset{⇀}{b}$ 表示为（）

A、 $\overset{⇀}{a} = 3 \overset{⇀}{b}$ B、 $\overset{⇀}{a} = - 3 \overset{⇀}{b}$ C、 $\overset{⇀}{a} = \frac{1}{3} \overset{⇀}{b}$ D、 $\overset{⇀}{a} = - \frac{1}{3} \overset{⇀}{b}$

查看试题解析
4. 在△ABC中，∠C＝90°，AB＝2，AC＝1，则cosB的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、2

查看试题解析
5. 下列各组条件中，一定能推得△ABC与△DEF相似的是（　　）

A、∠A=∠E且∠D=∠F B、∠A=∠B且∠D=∠F C、∠A=∠E且 $\frac{A B}{A C} = \frac{E F}{E D}$ D、∠A=∠E且 $\frac{A B}{B C} = \frac{D F}{E D}$

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，那么下列结论中正确的是（）

A、 $a c > 0$ B、当 $x > - 1$ 时， $y > 0$ C、 $b = 2 a$ D、 $9 a + 3 b + c = 0$

查看试题解析

二、填空题

7. 如果 $\frac{x - y}{y} = \frac{2}{3}$ ，那么 $\frac{x}{y} =$ ．

查看试题解析
8. 计算： $2 (3 \vec{a} + 2 \vec{b}) - 5 \vec{a} =$ ．

查看试题解析
9. 已知线段AB＝8cm，点C是AB的黄金分割点，且 $A C > B C$ ，那么线段AC的长为cm．

查看试题解析
10. 如果抛物线 $y = (k - 2) x^{2}$ 的开口向上，那么k的取值范围是．

查看试题解析
11. 如果抛物线 $y = - x^{2} + 3 x - 1 + m$ 经过原点，那么m=.

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 自变量x的值和它对应的函数值y如下表所示：
x
…
1
0
1
2
3
…
y
…
0
3
4
3
m
…
那么上表中m的值为．

查看试题解析
13. 某滑雪运动员沿着坡比为1： $\sqrt{3}$ 的斜坡向下滑行了100米，则运动员下降的垂直高度为米．

查看试题解析
14. 如图，直线 $A D ∥ B E ∥ C F$ ，如果 $\frac{A B}{B C} = \frac{1}{3}$ ， $A D = 2$ ， $C F = 6$ ，那么线段BE的长是．

查看试题解析
15. 如图，在平行四边形ABCD中，点M是边CD中点，点N是边BC的中点，设 $A B = \vec{a}$ ， $B C = \vec{b}$ ，那么 $\vec{M N}$ 可用 $\vec{a}$ ， $\vec{b}$ 表示为．

查看试题解析
16. 如图，已知正方形DEFG的顶点D、E在△ABC的边BC上，顶点G、F分别在边AB、AC上．如果BC=4，△ABC的面积是6，那么这个正方形的边长是．

查看试题解析
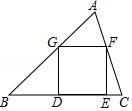17. 定义：有一组对边相等而另一组对边不相等的凸四边形叫做“对等四边形”，如图，在 $R t △ P B C$ 中， $∠ P C B = 90 °$ ，点A在边BP上，点D在边CP上，如果 $B C = 11$ ， $t a n ∠ P B C = \frac{12}{5}$ ， $A B = 13$ ，四边形ABCD为“对等四边形”，那么CD的长为．

查看试题解析
18. 如图所示，在三角形纸片ABC中，AB＝9，BC＝6，∠ACB＝2∠A，如果将 $△ A B C$ 沿过顶点C的直线折叠，使点B落在边AC上的点D处，折痕为CM，那么 $c o s ∠ D M A =$ ．

查看试题解析

三、解答题

19. 计算： $3 t a n 30 ° + 2 c o s 45 ° - 2 s i n 60 ° \times c o t 45 °$

查看试题解析
20. 如图，在 $△ A B C$ 中，点F为 $△ A B C$ 的重心，联结AF并延长交BC于点D，联结BF并延长交AC于点E．

(1)、求 $\frac{S_{△ D E F}}{S_{△ A B F}}$ 的值；

(2)、如果 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，用 $\vec{a}$ ， $\vec{b}$ 表示 $\vec{B E}$ 和 $\vec{A F}$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C = \sqrt{5}$ ， $s i n B = \frac{2 \sqrt{5}}{5}$ ．

(1)、求边BC的长度；

(2)、求 $c o s A$ 的值．

查看试题解析
22. 如图，小明同学在学习了解直角三角形及其应用的知识后，尝试利用无人机测量他所住小区的楼房BC的高度，当无人机在地面A点处时，测得小区楼房BC顶端点C处的仰角为30°，当无人机垂直向上飞行到距地面60米的D点处时，测得小区楼房BC顶端点C处的俯角为45°．

(1)、求小区楼房BC的高度；

(2)、若无人机保持现有高度沿平行于AB的方向，并以5米/秒的速度继续向前匀速飞行，问：经过多少秒后，无人机无法观察到地面上点A的位置（计算结果保留根号）

查看试题解析
23. 已知：如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，垂足为点D，E为边AC上一点，联结BE交CD于点F，并满足 $B C^{2} = C D \cdot B E$ ．求证：

(1)、 $△ B C E ∽ △ A C B$ ；

(2)、过点C作 $C M ⊥ B E$ ，交BE于点G，交AB于点M，求证： $B E \cdot C M = A B \cdot C F$ ．

查看试题解析
24. 如图，抛物线y=− $\frac{3}{4}$ x²+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．

(1)、求抛物线的解析式，并写出此抛物线的对称轴和顶点坐标；

(2)、如果以点P、N、B、O为顶点的四边形为平行四边形，求m的值；

(3)、如果以B、P、N为顶点的三角形与△ABO相似，求点M的坐标．

查看试题解析
25. 已知：如图，正方形的边长为1，在射线AB上取一点E，联结DE，将ADE绕点D针旋转90°，E点落在点F处，联结EF，与对角线BD所在的直线交于点M，与射线DC交于点N．求证：

(1)、当 $A E = \frac{1}{3}$ 时，求 $t a n ∠ E D B$ 的值；

(2)、当点E在线段AB上，如果 $A E = x$ ， $F M = y$ ，求y关于x的函数解析式，并写出定义域；

(3)、联结AM，直线AM与直线BC交于点G，当 $B G = \frac{1}{3}$ 时，求AE的值．

查看试题解析

x	…	1	0	1	2	3	…
y	…	0	3	4	3	m	…