上海市宝山区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $\frac{a}{b} = \frac{2}{3}$ ，且 $b$ 是 $a$ 和 $c$ 的比例中项，那么 $\frac{b}{c}$ 等于（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 在比例尺为 $1 ： 5000$ 的地图上，如果 $A 、 B$ 两地的距离是10厘米，那么这两地的实际距离是（）

A、50000米 B、5000米 C、500米 D、50米

查看试题解析
3. 已知 $c$ 为非零向量， $a = 2 c ， b = - 3 c$ ，那么下列结论中，不正确的是（）

A、 $| a | = \frac{2}{3} | b |$ B、 $a = - \frac{3}{2} b$ C、 $3 a + 2 b = 0$ D、 $\vec{a} ∥ \vec{b}$

查看试题解析
4. 如图，已知Rt $△ A B C ， C D$ 是斜边 $A B$ 边上的高，那么下列结论正确的是（）

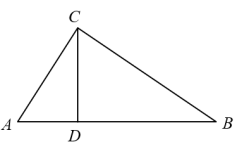A、 $C D = A B \cdot t a n B$ B、 $C D = A D \cdot c o t A$ C、 $C D = A C \cdot s i n B$ D、 $C D = B C \cdot c o s A$

查看试题解析
5. 把抛物线 $y = {(x - 1)}^{2} + 3$ 向左平移2个单位长度，平移后抛物线的表达式为（）

A、 $y = {(x - 1)}^{2} + 5$ B、 $y = {(x - 1)}^{2} + 1$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x - 3)}^{2} + 3$

查看试题解析
6. 下列格点三角形中，与右侧已知格点 $△ A B C$ 相似的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 已知点 $B$ 在线段 $A C$ 上， $A B = 2 B C$ ，那么 $A C ： A B$ 的比值是．

查看试题解析
8. 如果 $\frac{x - y}{y}$ 的值是黄金分割数，那么 $\frac{x}{y}$ 的值为．

查看试题解析
9. 计算： $s i n^{2} 3 0^{∘} ＋ c o s^{2} 4 5^{∘} ＝$ ．

查看试题解析
10. 在Rt $△ A B C$ 中， $∠ C = 9 0^{∘}$ ，如果 $\frac{A C}{B C} = \frac{3}{4}$ ，那么 $s i n A$ 的值是．

查看试题解析
11. 已知二次函数 $y = \frac{1}{3} x^{2} + x - 1$ ，当 $x = - 3$ 时，函数 $y$ 的值是．

查看试题解析
12. 据了解，某蔬菜种植基地2019年的蔬菜产量为100万吨，2021年的蔬菜产量为 $y$ 万吨，如果2019年至2021年蔬菜产量的年平均增长率为 $x (x > 0)$ ，那么y关于x的函数解析式为．

查看试题解析
13. 如果抛物线 $y = x^{2} + 2 x + m - 1$ 的顶点在 $x$ 轴上，那么 $m$ 的值是．

查看试题解析
14. 已知 $△ A B C$ 的两条中线 $A D 、 B E$ 相交于点 $F$ 如果 $A F ＝ 10$ ，那么 $A D$ 的长为．

查看试题解析
15. 如图，一段铁路路基的横断面为等腰梯形，路基的上底宽AD为3米，路基高为1米，斜坡AB的坡度 $= 1 ： 1.5$ ，那么路基的下底宽BC是米．

查看试题解析
16. 如图，已知一张三角形纸片 $A B C ， A B = 5 ， B C = 2 ， A C = 4$ ，点 $M$ 在 $A C$ 边上．如果过点 $M$ 剪下一个与 $△ A B C$ 相似的小三角形纸片，可以有四种不同的剪法，设 $A M = x$ ，那么 $x$ 的取值范围是．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = 3 ， B C = 5$ ，点 $P$ 在 $C D$ 边上，联结 $A P$ ．如果将 $△ A D P$ 沿直线 $A P$ 翻折，点 $D$ 恰好落在线段 $B C$ 上，那么 $\frac{S_{△ A D P}}{S_{四边形 A B C P}}$ 的值为．

查看试题解析
18. 如果一条抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条拋物线的“特征三角形”．已知 $y = x^{2} + b x (b > 0)$ 的“特征三角形”是等腰直角三角形，那么 $b$ 的值为．

查看试题解析

三、解答题

19. 如图，在 $△ A B C$ 中， $A B = A C = 5 ， B C = 6$

(1)、求tanB的值；

(2)、延长BC至点D，联结AD，如果∠ADB＝30°，求CD的长．

查看试题解析
20. 如图，已知在四边形ABCD中，F是边AD上一点， $A F = 2 D F$ ， BF交AC于点E， $\vec{A F} = \frac{1}{4} \vec{B C}$ ．

(1)、设 $\vec{A B} = a ， \vec{A D} = b$ ，用向量 $a 、 b$ 表示向量 $\vec{B F}$ =； $\vec{A C}$ =

(2)、如果 $∠ A B C = 9 0^{°} ， A D = 3 ， A B = 4$ 求 $B E$ 的长．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，已知二次函数图象的顶点为 $A (- 1 ， 2)$ ，且经过 $B (- 3 ， 0)$ ．

(1)、求二次函数的解析式；

(2)、将该二次函数图象向右平移几个单位，可使平移后所得图像经过坐标原点？并直接写出平移后所得图像与 $x$ 轴的另一个交点的坐标．

查看试题解析
22. 如图，小杰在湖边高出水面 $M N$ 约 $10 m$ 的平台A处发现一架无人机停留在湖面上空的点P处，该无人机在湖中的倒影为点 $P'$ ，小杰在A处测得点P的仰角为 $45 °$ ，点 $P'$ 的俯角为60 $°$ ，求该无人机离开湖面的高度（结果保留根号）．

查看试题解析
23. 如图，已知 $△ A B C$ 和 $△ D C E$ 都是等边三角形，点 $B 、 C 、 E$ 在同一直线上，联结 $B D$ 交 $A C$ 边于点 $F$ ．

(1)、如果 $∠ A B D = ∠ C A D$ ，求证： $B F^{2} = D F \cdot D B$ ；

(2)、如果 $A F = 2 F C ， S_{四边形 A B C D} = 18$ ，求 $S_{△ D C F}$ 的值．

查看试题解析
24. 已知在平面直角坐标系 $x O y$ 中，拋物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过点 $A (- 1 ， 0)$ 、 $B (3 ， 0) ， C (0 ， 3)$ ，顶点为点 $D$ ．

(1)、求抛物线的表达式及顶点 $D$ 的坐标；

(2)、联结 $B D 、 C D$ ，试判断 $△ B C D$ 与 $△ A O C$ 是否相似，并证明你的结论；

(3)、抛物线上是否存在点 $P$ ，使得 $∠ P A C = 4 5^{∘}$ ．如果存在，请求出点 $P$ 的坐标；如果不存在，请说明理由．

查看试题解析
25. 如图，已知正方形ABCD，将AD绕点A逆时针方向旋转 $n ° (0 < n < 90)$ 到AP的位置，分别过点 $C 、 D$ 作 $C E ⊥ B P ， D F ⊥ B P$ ，垂足分别为点 $E$ 、 $F$ ．

(1)、求证： $C E = E F$ ；

(2)、联结 $C F$ ，如果 $\frac{D P}{C F} = \frac{1}{3}$ ，求 $∠ A B P$ 的正切值；

(3)、联结 $A F$ ，如果 $A F = \frac{\sqrt{2}}{2} A B$ ，求 $n$ 的值．

查看试题解析