山西省太原市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各点中，在反比例函数 $y = \frac{4}{x}$ 图象上的点是（）

A、（4，1） B、（2，﹣2） C、（﹣1，4） D、（2，3）

查看试题解析
2. 如图是一个几何体的三种视图，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
3. 如图，直线l₁ $∥$ l₂ $∥$ l₃ ，分别交直线m，n于点A，B，C，D，E，F．已知AB＝4，BC＝6，DE＝2，则EF的长为（）

A、2 B、3 C、4 D、4.5

查看试题解析
4. 将图1所示的长方形纸片对折后得到图2，图2再对折后得到图3，沿图3中的虚线剪下并展开，所得的四边形是（）

A、矩形 B、菱形 C、正方形 D、梯形

查看试题解析
5. 一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了200次球，发现有140次摸到红球，由此估计这个口袋中红球的个数为（）

A、3个 B、4个 C、6个 D、7个

查看试题解析
6. 如图，矩形ABCD的对称轴分别交AB于点E，交CD于点F．若矩形AEFD与矩形ABCD相似，则AB：BC的值为（）

A、2 B、 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
7. 已知A（7，y₁）和B（2，y₂）是反比例函数 $y = \frac{7}{x}$ 图象上的两点，则y₁与y₂的大小关系是（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、无法确定

查看试题解析
8. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC＝12，BD＝16，则菱形的高AE为（）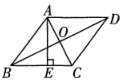

A、9.6 B、4.8 C、10 D、5

查看试题解析
9. 学校计划在长为12m，宽为9m矩形地块的正中间建一座劳动实践大棚．大棚是占地面积为88m²的矩形．建成后，大棚外围留下宽度都相同的区域，这个宽度应设计为（）

A、1.8m B、1.5m C、1m D、0.5m

查看试题解析
10. 如图，在平面直角坐标系中，四边形ABCD与四边形A'B'C'D'是位似图形．位似中心是（）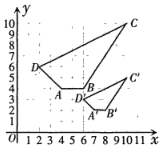

A、（8，0） B、（8，1） C、（10，0） D、（10，1）

查看试题解析
11. 如图，在平面直角坐标系中，四边形ABCD与四边形A'B'C'D'是位似图形．位似中心到点D和点D'的距离的比值是（）

A、2 B、 $\sqrt{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{4}$

查看试题解析

二、填空题

12. 添加一个条件，使矩形ABCD是正方形，这个条件可能是．

查看试题解析
13. 在 $Δ A B C$ 中，∠C= $90 °$ ， AC=12，BC=5，则AB边上的中线CD= ．

查看试题解析
14. 已知，△ABC∽△A'B'C'， $\frac{A C}{A C} = \frac{3}{2}$ ， △ABC的面积为45，则△A'B'C'的面积等于．

查看试题解析
15. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm．他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像．蜡烛应放在距离纸筒 cm的地方．

查看试题解析
16. 如图，在平面直角坐标系中，矩形ABCD的顶点A，C分别在x轴的负半轴上，y轴的正半轴上，y轴平分AB边，点A的坐标（﹣2，0），AB＝5．过点B的反比例函数的表达式是．

查看试题解析
17. 如图，在平面直角坐标系中，矩形ABCD的顶点A，C分别在x轴的负半轴上，y轴的正半轴上，y轴平分AB边，点A的坐标（﹣2，0），AB＝5．过点D的反比例函数的表达式是．

查看试题解析

三、解答题

18. 解方程：

(1)、（x﹣4）（5x+7）＝0；

(2)、x²﹣4x﹣6＝0．

查看试题解析
19. 如图，一个广告牌挡住了路灯的灯泡．小李、小张、路灯的灯杆及小赵在同一平面内．

(1)、画出该路灯灯泡所在的位置O；

(2)、画出表示小赵身高的线段AB．

查看试题解析
20. 如图，在平行四边形ABCD中，点M是AD边的中点，连接BM，CM，且BM＝CM．

(1)、求证：四边形ABCD是矩形；

(2)、若△BCM是直角三角形，直接写出AD与AB之间的数量关系．

查看试题解析
21. 小颖为元旦联欢会设计了一个“配紫色”游戏：如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形．游戏者同时转动两个转盘，如果一个转盘转出了红色，另一个转盘转出了蓝色，那么游戏者获胜，因为红色和蓝色在一起配成了紫色．如果转盘的指针落在分割线上，则重新转动转盘．用列表或画树状图的方法，求游戏者获胜的概率．

查看试题解析
22. 市政府计划建设一项惠民工程，工程需要运送的土石方总量为10⁵m³ ，经招投标后，先锋运输公司承担了运送土石方的任务．

(1)、直接写出运输公司平均每天运送速度v（单位：m³/天）与完成任务所需时间t（单位：天）之间的函数关系式；

(2)、如果每辆车每天平均运送10²m³的土石方，要求不超过50天完成任务，求运输公司平均每天至少安排多少辆车．

查看试题解析
23. 如图，在△ACB中，AC=30cm，BC=25cm．动点P从点C出发，沿CA向终点A匀速运动，速度是2cm/s；同时，动点Q从点B出发，沿BC向终点C匀速运动，速度是1cm/s．当△CPQ与△CAB相似时，求运动的时间．

查看试题解析
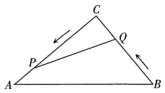24. 第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕，北京成为历史上第一个既举办夏奥会又举办冬奥会的城市．某批发商最近订购了一批具有纪念意义的书签进行销售，平均每天可售出500张，每张可获利0.5元．调查发现，如果每张书签的售价每降价0.1元，平均每天可多售出200张．批发商要想平均每天获利270元，求每张书签应降价多少元．

查看试题解析
25. 如图，正比例函数y₁＝kx与反比例函数y₂＝ $\frac{m}{x}$ 的图象相交于点A（2，4）和点B，点C的坐标是（4，0），点D在y₂＝ $\frac{m}{x}$ 的图象上．

(1)、求反比例函数的表达式；

(2)、设点E在x轴上，∠AEB＝90°，求点E的坐标；

(3)、设点M在x轴上，点N在平面直角坐标系内．当四边形CDNM是正方形时，直接写出点M的坐标．

查看试题解析