山东省青岛市市南区东部联考2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 如图是一根空心方管,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 万花筒写轮眼是漫画《火影忍者》及其衍生作品中的一种瞳术,下列图标中,是中心对称图形的有( )个
2. 万花筒写轮眼是漫画《火影忍者》及其衍生作品中的一种瞳术,下列图标中,是中心对称图形的有( )个 A、2 B、3 C、4 D、53. 今年元旦期间,某种女服装连续两次降价处理,由每件200元调至72元,设平均每次的降价百分率为 ,则得方程( )A、 B、 C、 D、4. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=: , 则四边形ABCD和A′B′C′D′的面积比为( )
A、2 B、3 C、4 D、53. 今年元旦期间,某种女服装连续两次降价处理,由每件200元调至72元,设平均每次的降价百分率为 ,则得方程( )A、 B、 C、 D、4. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=: , 则四边形ABCD和A′B′C′D′的面积比为( )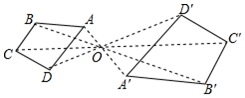 A、: B、2:3 C、2:5 D、4:95. 如图,已知抛物线l1:y=(x﹣2)2﹣4与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为12,则抛物线l2的函数表达式为( )
A、: B、2:3 C、2:5 D、4:95. 如图,已知抛物线l1:y=(x﹣2)2﹣4与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为12,则抛物线l2的函数表达式为( ) A、y=(x﹣2)2﹣1 B、y=(x﹣2)2+1 C、y=(x﹣2)2﹣2 D、y=(x﹣2)2+26. 如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为 )
A、y=(x﹣2)2﹣1 B、y=(x﹣2)2+1 C、y=(x﹣2)2﹣2 D、y=(x﹣2)2+26. 如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为 )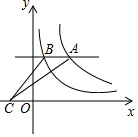 A、8 B、-8 C、4 D、-47. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )
A、8 B、-8 C、4 D、-47. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )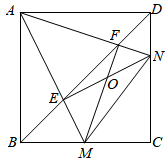 A、①②③ B、①②④ C、②③④ D、①②③④8. 已知a,b是非零实数,|b|>|a|,二次函数y1=ax2﹣bx与一次函数y2=ax﹣b的大致图象不大可能的是( )A、
A、①②③ B、①②④ C、②③④ D、①②③④8. 已知a,b是非零实数,|b|>|a|,二次函数y1=ax2﹣bx与一次函数y2=ax﹣b的大致图象不大可能的是( )A、 B、
B、 C、
C、 D、
D、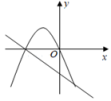
二、填空题
-
9. 计算的结果为 .10. 如图,点A(3,4),点B(4,0),以O为位似中心,按比例1∶2,将△AOB放大后得△A1O1B1 , 则A1坐标为 .
 11. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.
11. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.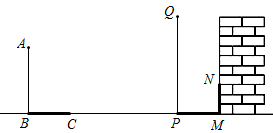 12. 如图,△ABC的顶点A,B都在反比例函数y=﹣ , 点C(0,3),且AC=BC, , 则线段AB的长为 .
12. 如图,△ABC的顶点A,B都在反比例函数y=﹣ , 点C(0,3),且AC=BC, , 则线段AB的长为 . 13. 如图,正方形ABCD的边长为4,对角线AC,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,点G为EF中点,连接OE,交CD于点H,则GH的长为 .
13. 如图,正方形ABCD的边长为4,对角线AC,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,点G为EF中点,连接OE,交CD于点H,则GH的长为 . 14. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A′B′的中点,若BC=2,∠BAC=30°,则线段PM的最大值是 .
14. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A′B′的中点,若BC=2,∠BAC=30°,则线段PM的最大值是 .
三、解答题
-
15. 要求:请用直尺、圆规作图,不写作法,但要保留作图痕迹.
在△ABC中,∠ABC=80°,∠ACB=60°,求作 , 使得△ABC∽△BDC.
 16.(1)、计算:2cos230°﹣sin45°+2tan60°•tan45°;(2)、利用公式法解下列方程:(x+2)(2x﹣3)=3x+2.17. 为落实“十个一”活动,学校组建了多个志愿者服务队,小盖和小吕通过做游戏决定谁优先选择服务队,游戏规则:两人各掷一次质地均匀的骰子,如果掷出的点数之和是小于7的偶数,由小盖优先选择服务队;如果掷出的点数之和是大于6的奇数,由小吕优先选择服务队,请利用画树状图或列表的方法,判断这个游戏对双方是否公平.18. 《攀登者》于2019年9月30日在中国内地上映.展现出了中国登山队为了国家使命勇于攀登的精神.在2021年4月30日,一支登山队再一次成功地登上了珠峰之巅,站上了珠峰顶部.已知一个人登山时的动作可以简化成下图所示,他的大腿长AB=AC=45cm,上坡时大腿之间的夹角∠BAC=65°,某段山坡DF的坡度为i= , 大约走多少步才能将自己所处位置的海拔提高50米?
16.(1)、计算:2cos230°﹣sin45°+2tan60°•tan45°;(2)、利用公式法解下列方程:(x+2)(2x﹣3)=3x+2.17. 为落实“十个一”活动,学校组建了多个志愿者服务队,小盖和小吕通过做游戏决定谁优先选择服务队,游戏规则:两人各掷一次质地均匀的骰子,如果掷出的点数之和是小于7的偶数,由小盖优先选择服务队;如果掷出的点数之和是大于6的奇数,由小吕优先选择服务队,请利用画树状图或列表的方法,判断这个游戏对双方是否公平.18. 《攀登者》于2019年9月30日在中国内地上映.展现出了中国登山队为了国家使命勇于攀登的精神.在2021年4月30日,一支登山队再一次成功地登上了珠峰之巅,站上了珠峰顶部.已知一个人登山时的动作可以简化成下图所示,他的大腿长AB=AC=45cm,上坡时大腿之间的夹角∠BAC=65°,某段山坡DF的坡度为i= , 大约走多少步才能将自己所处位置的海拔提高50米?(结果保留两位小数,sin65°≈ , tan65°≈ , cos65°≈)
 19. “福虎迎冬奥”明溪喜迎冬奥篮球赛火热开启,运动员你攻我守,分秒必争,篮球运动员小明站在点O处长抛球,球从离地面1米的A处扔出,篮球在距O点6米的B处达到最高点,最高点C距地面4米,又一次弹起,落到点E处,EF之间的距离为2米,据试验,篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同,但最大高度减少到原来最大高度的一半,以小明站立处O为坐标原点,建立平面直角坐标系如图所示.(算出的结果均保留整数,≈1.75;≈2.5)
19. “福虎迎冬奥”明溪喜迎冬奥篮球赛火热开启,运动员你攻我守,分秒必争,篮球运动员小明站在点O处长抛球,球从离地面1米的A处扔出,篮球在距O点6米的B处达到最高点,最高点C距地面4米,又一次弹起,落到点E处,EF之间的距离为2米,据试验,篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同,但最大高度减少到原来最大高度的一半,以小明站立处O为坐标原点,建立平面直角坐标系如图所示.(算出的结果均保留整数,≈1.75;≈2.5) (1)、求抛物线ACD的函数表达式;(2)、篮球第二次落地点E距O点的距离;(3)、若小明需要在第一次抛球时投中篮筐,他应该向前走多远?20. 按时饮水,对人体有很多好处,可以补充人体必需的水分,该饮水机的工作程序是:放满水后,接通电源,每分钟水温上升10℃,待加热到100℃,水温开始下降,水温y(℃)(min)成反比例关系,直至水温降至室温,重复上述过程.设某天水温和室温为20℃,接通电源后,回答下列问题:
(1)、求抛物线ACD的函数表达式;(2)、篮球第二次落地点E距O点的距离;(3)、若小明需要在第一次抛球时投中篮筐,他应该向前走多远?20. 按时饮水,对人体有很多好处,可以补充人体必需的水分,该饮水机的工作程序是:放满水后,接通电源,每分钟水温上升10℃,待加热到100℃,水温开始下降,水温y(℃)(min)成反比例关系,直至水温降至室温,重复上述过程.设某天水温和室温为20℃,接通电源后,回答下列问题:时间
节次
上
午
7:20
到校
7:45~8:20
第一节
8:30~9:05
第二节
……
……
 (1)、分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;(2)、求出图中a的值;(3)、下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)21. 如图,已知▱ABCD,E为BC边上的垂直平分线,BF=BC=2AB,且∠ABD=90°.
(1)、分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;(2)、求出图中a的值;(3)、下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)21. 如图,已知▱ABCD,E为BC边上的垂直平分线,BF=BC=2AB,且∠ABD=90°. (1)、求证:△ABD≌△CEF;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.22. 生态水果是指在保护、改善农业生态环境的前提下,遵循生态学、生态经济学规律,运用现代科学技术,营养的、健康的水果.青岛市扶贫工作小组对李沧、胶州、即墨等多地果农进行精准投资建设,帮助果农将一种有机生态水果拓宽了市场,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了 . 批发销售总额比去年增加了20%(1)、已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?(2)、今年某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克.设水果店一天的利润为w元,当每千克的平均销售价为多少元时该水果店一天的利润最大(利润计算时,其它费用忽略不计,并且售价为整数)23. 【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点C为线段AB的黄金分割点.
(1)、求证:△ABD≌△CEF;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.22. 生态水果是指在保护、改善农业生态环境的前提下,遵循生态学、生态经济学规律,运用现代科学技术,营养的、健康的水果.青岛市扶贫工作小组对李沧、胶州、即墨等多地果农进行精准投资建设,帮助果农将一种有机生态水果拓宽了市场,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了 . 批发销售总额比去年增加了20%(1)、已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?(2)、今年某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克.设水果店一天的利润为w元,当每千克的平均销售价为多少元时该水果店一天的利润最大(利润计算时,其它费用忽略不计,并且售价为整数)23. 【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点C为线段AB的黄金分割点.
 (1)、【问题发现】如图1,请直接写出AC与CB的比值是 .(2)、【问题探究】如图2,在Rt△ABC中,∠C=90°,BC=1, , 在BA上截取BD=BC,在上截取 , 则的值为 .(3)、【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE得折痕MN,连接EN,点A对应点H,得折痕CE,试说明:C是AB的黄金分割点;(4)、【拓展延伸】如图4,正方形ABCD中,M为对角线BD上一点,点N在边CD上,且CN<DN,当N为CD的黄金分割点时,∠AMB=∠ANB,连NM,延长NM交AD于E,请用相似的知识求出的值为 .24. 如图,△ADB与△BCD均为等边三角形,延长AD到E,使∠AEC=90°,AD=5,动点M从点B出发,沿BD方向运动,移动速度为1个单位/秒,同时,点N由点D向点C运动,移动速度为2个单位/秒,其中一个到终点,都停止运动,连接AM,CM,MN,NE,设运动时间为t(0≤t≤2.5)
(1)、【问题发现】如图1,请直接写出AC与CB的比值是 .(2)、【问题探究】如图2,在Rt△ABC中,∠C=90°,BC=1, , 在BA上截取BD=BC,在上截取 , 则的值为 .(3)、【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE得折痕MN,连接EN,点A对应点H,得折痕CE,试说明:C是AB的黄金分割点;(4)、【拓展延伸】如图4,正方形ABCD中,M为对角线BD上一点,点N在边CD上,且CN<DN,当N为CD的黄金分割点时,∠AMB=∠ANB,连NM,延长NM交AD于E,请用相似的知识求出的值为 .24. 如图,△ADB与△BCD均为等边三角形,延长AD到E,使∠AEC=90°,AD=5,动点M从点B出发,沿BD方向运动,移动速度为1个单位/秒,同时,点N由点D向点C运动,移动速度为2个单位/秒,其中一个到终点,都停止运动,连接AM,CM,MN,NE,设运动时间为t(0≤t≤2.5) (1)、t为何值时,MN∥BC;(2)、连接BN,t为何值时,BNE三点共线;(3)、设四边形AMNE的面积为S,求S与t的函数关系式;(4)、是否存在某一时刻t,使N在∠CMD的角平分线上,若存在,求出t近似值;若不存在,说明理由.
(1)、t为何值时,MN∥BC;(2)、连接BN,t为何值时,BNE三点共线;(3)、设四边形AMNE的面积为S,求S与t的函数关系式;(4)、是否存在某一时刻t,使N在∠CMD的角平分线上,若存在,求出t近似值;若不存在,说明理由.