山东省济宁市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 6的相反数是（）

A、 $- \frac{1}{6}$ B、 $\frac{1}{6}$ C、-6 D、6

查看试题解析
2. 到2020年底，我国完成了“脱贫攻坚”任务，有约9980万的贫困人口实现了脱贫.将数据9980万用科学记数法表示是（）

A、 $9.98 \times 10^{3}$ B、 $9.98 \times 10^{5}$ C、 $9.98 \times 10^{6}$ D、 $9.98 \times 10^{7}$

查看试题解析
3. 2021年是农历辛丑牛年，习近平总书记勉励全国各族人民在新的一年发扬“为民服务孺子牛、创新发展拓荒牛、艰苦奋斗老黄牛”精神，某社区也开展了“迎新春牛年剪纸展”，下面的剪纸作品是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知 $10^{a} = 20$ ， $100^{b} = 50$ ，则 $\frac{1}{2} a + b + \frac{3}{2}$ 的值是（）

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{9}{2}$

查看试题解析
5. 若长度分别是a、3、5的三条线段能组成一个三角形，则a的值可以是（）

A、1 B、2 C、4 D、8

查看试题解析
6. 在一次演讲比赛中，七位评委为某位选手打出的分数如下：95，94，96，99，93，97，90（单位：分）．若去掉一个最高分和一个最低分．则去掉前与去掉后没有改变的一个统计量是（）

A、平均分 B、方差 C、极差 D、中位数

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ B = 45 ° ， ∠ C = 60 ° ， A D ⊥ B C$ 于点D， $B D = \sqrt{3}$ .若E，F分别为 $A B$ ， $B C$ 的中点，则 $E F$ 的长为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\frac{\sqrt{6}}{2}$

查看试题解析
8. 已知 $9^{m} = 3 ， 27^{n} = 4$ ，则 $3^{2 m + 3 n} =$ （）

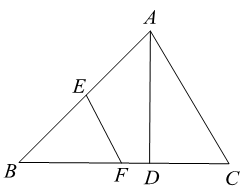A、1 B、6 C、7 D、12

查看试题解析
9. 如图， $A B$ 、 $B C$ 、 $C D$ 、 $D E$ 是四根长度均为5cm的火柴棒，点A、C、E共线.若 $A C = 6 cm$ ， $C D ⊥ B C$ ，则线段 $C E$ 的长度为（）

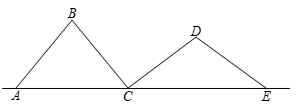A、6 cm B、7 cm C、 $6 \sqrt{2} cm$ D、8cm

查看试题解析
10. 按如图所示的运算程序，能使输出的b的值为﹣1的是（）

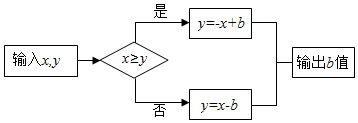A、x＝1，y＝2 B、x＝2，y＝0 C、x＝2，y＝1 D、x＝﹣1，y＝1

查看试题解析

二、填空题

11. 已知关于 $x$ 的一元二次方程 $x^{2} + 6 x + k = 0$ 有两个相等的实数根，则实数 $k$ 的值为.

查看试题解析
12. 现有4张卡片，正面图案如图所示，它们除此之外完全相同，把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案恰好是“天问”和“九章”的概率是．

查看试题解析
13. 如图，已知AB＝DE，∠B＝∠E，请你添加一个适当的条件（填写一个即可），使得△ABC≌△DEC.

查看试题解析
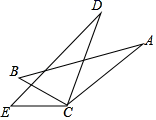14. 设M＝x+y，N＝x﹣y，P＝xy．若M＝1，N＝2，则P＝．

查看试题解析
15. 在平面直角坐标系中，对于不在坐标轴上的任意一点 $A (x ， y)$ ，我们把点 $B (\frac{1}{x} ， \frac{1}{y})$ 称为点A的“倒数点”.如图，矩形 $O C D E$ 的顶点C为 $(3 ， 0)$ ，顶点E在y轴上，函数 $y = \frac{2}{x} (x > 0)$ 的图象与 $D E$ 交于点A.若点B是点A的“倒数点”，且点B在矩形 $O C D E$ 的一边上，则 $△ O B C$ 的面积为.

查看试题解析

三、解答题

16. 先化简，再求值：
$(\frac{2 x + 1}{x + 1} + x - 1) \div \frac{x + 2}{x^{2} + 2 x + 1}$ ，其中x满足 $x^{2} - x - 2 = 0$ ．

查看试题解析
17. 感恩是中华民族的传统美德，学校在3月份提出了“感恩父母、感恩老师、感恩他人”感恩在行动教育活动．感恩行动有：A．由你为父母过一次有意义的生日；B．为班级设计一个班徽；C．主动找老师进行一次交流，谈一谈自己对于未来的憧憬；D．关注身边有需要帮助的同学，帮助有困难的同学渡过难关．为了了解学生对这4种感恩行动的选择情况，学校德育处在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的学生在4种感恩行动中只选择最喜欢做的一种），将数据进行整理并绘制成如下两幅统计图（未画完整）．

(1)、这次调查中，一共调查了名学生；

(2)、请补全扇形统计图中的数据及条形统计图；

(3)、本次九（1）班被抽样的学生一共5名同学，其中3名是选A的同学，1名是选C的同学，1名是选D的同学，班委会准备组织一次主题班会，要从这5名同学中随机选出2人在班会上介绍自己的行动方案，请通过树状图或列表求两人均是选A的概率．

查看试题解析
18. 如图，线段 $E F$ 与 $M N$ 表示某一段河的两岸， $E F // M N$ ．综合实践课上，同学们需要在河岸 $M N$ 上测量这段河的宽度（ $E F$ 与 $M N$ 之间的距离），已知河对岸 $E F$ 上有建筑物C、D ，且 $C D = 60$ 米，同学们首先在河岸 $M N$ 上选取点A处，用测角仪测得C建筑物位于A北偏东45°方向，再沿河岸走20米到达B处，测得D建筑物位于B北偏东55°方向，请你根据所测数据求出该段河的宽度，（用非特殊角的三角函数或根式表示即可）

查看试题解析
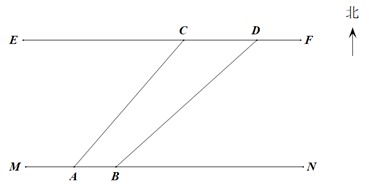19. 随着我国科技事业的不断发展，国产无人机大量进入快递行业.现有A，B两种型号的无人机都被用来运送快件，A型机比B型机平均每小时多运送20件，A型机运送700件所用时间与B型机运送500件所用时间相等，两种无人机平均每小时分别运送多少快件？

查看试题解析
20. 如图，AB是⊙O的直径，点E、F在⊙O上，且 $\overset{⌢}{B F}$ ＝2 $\overset{⌢}{B E}$ ，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．

(1)、求证：∠COB＝∠A；

(2)、若AB＝6，CB＝4，求线段FD的长．

查看试题解析
21. 阅读以下材料，苏格兰数学家纳皮尔（J.Npler，1550－1617年）是对数的创始人，他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler.1707－1783年）才发现指数与对数之间的联系.
对数的定义：一般地.若 $a^{x} = N$ （ $a > 0$ 且 $a \neq 1$ ），那么x叫做以a为底N的对数，

记作 $x = \log_{a} N$ ，比如指数式 $2^{4} = 16$ 可以转化为对数式 $4 = \log_{2} 16$ ，对数式 $2 = \log_{3} 9$ 可以转化为指数式 $3^{2} = 9$ .我们根据对数的定义可得到对数的一个性质：

$\log_{a} (M \cdot N) = \log_{a} M + \log_{a} N (a > 0 ， a \neq 1 ， M > 0 ， N > 0)$ ，理由如下：

设 $\log_{a} M = m ， \log_{a} N = n$ ，则 $M = a^{m} ， N = a^{n}$ .

$∴ M \cdot N = a^{m} \cdot a^{n} = a^{m + n}$ .由对数的定义得 $m + n = \log_{a} (M \cdot N)$

又 $∵ m + n = \log_{a} M + \log_{a} N$

$∴ \log_{a} (M \cdot N) = \log_{a} M + \log_{a} N$ .

根据上述材料，结合你所学的知识，解答下列问题：

(1)、填空：① $\log_{2} 32 =$ ；② $\log_{3} 27 =$ ， ③ ${log}_{7} l =$ ；

(2)、求证： $\log_{a} \frac{M}{N} = \log_{a} M - \log_{a} N (a > 0 ， a \neq 1 ， M > 0 ， N > 0)$ ；

(3)、拓展运用：计算 $\log_{5} 125 + \log_{5} 6 - \log_{5} 30$ .

查看试题解析
22. 在平面直角坐标系中，我们定义直线y＝ax﹣a为抛物线y＝ax²+bx+c（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．已知抛物线y＝ax²+bx+c与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C，tan∠ABO＝ $\frac{2 \sqrt{3}}{3}$ ， B（1，0），点A横坐标为﹣2，BC＝4．

(1)、求抛物线的解析式，并写出顶点坐标；

(2)、如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；

(3)、当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上是否存在点F，使得以点 A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点 E、F的坐标；若不存在，请说明理由．

查看试题解析