山东省济南市长清区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 的值为( )A、1 B、-1 C、 D、2. 如图摆放的下列几何体中,左视图是圆的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若函数的图象经过点A(2,4),则的值为( )A、4 B、-2 C、8 D、-84. 分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )A、 B、 C、 D、5. 抛物线y=(x-1)2+2的顶点坐标是( )A、(1,2) B、(-1,2) C、(1,-2) D、(-1,-2)6. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )A、1∶2 B、1∶3 C、1∶4 D、1∶97. 若是关于的一元二次方程的一个解,则的值是( )A、6 B、5 C、4 D、38. 小华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为( )A、3.2米 B、4.8米 C、5.2米 D、5.6米9. 已知点 , , 都在反比例函数 的图象上,则 , , 的大小关系正确的是( )A、 B、 C、 D、10. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
3. 若函数的图象经过点A(2,4),则的值为( )A、4 B、-2 C、8 D、-84. 分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )A、 B、 C、 D、5. 抛物线y=(x-1)2+2的顶点坐标是( )A、(1,2) B、(-1,2) C、(1,-2) D、(-1,-2)6. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )A、1∶2 B、1∶3 C、1∶4 D、1∶97. 若是关于的一元二次方程的一个解,则的值是( )A、6 B、5 C、4 D、38. 小华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为( )A、3.2米 B、4.8米 C、5.2米 D、5.6米9. 已知点 , , 都在反比例函数 的图象上,则 , , 的大小关系正确的是( )A、 B、 C、 D、10. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( ) A、3米 B、 米 C、2米 D、1米11. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=bx+c在同一坐标系内的大致图象是( )
A、3米 B、 米 C、2米 D、1米11. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=bx+c在同一坐标系内的大致图象是( ) A、
A、 B、
B、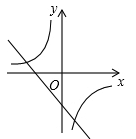 C、
C、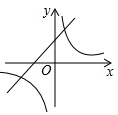 D、
D、 12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣ , 结合图象分析下列结论:①abc>0;②当x<0时,y随x的增大而增大;③3a+c>0;④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,其中正确的结论有( )
12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣ , 结合图象分析下列结论:①abc>0;②当x<0时,y随x的增大而增大;③3a+c>0;④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 已知 . 则= .14. 已知在Rt△ABC中,∠C=90°,AC=6,BC=8,则tanB等于 .15. 一个布袋里装有2个只有颜色不同的球,其中1个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球是一白一红的概率是 .16. 将抛物线先向下平移3个单位,再向左平移1个单位,则新的函数解析式为 .17. 如在平面直角坐标系中,等腰直角△ABO如图放置,直角顶点A在反比例函数的图形上,其中AB=AO,B(-2,0),则k= .
 18. 如图,正方形ABCD的边长为1,O为对角线BD的中点,点M在边AB上,且BM=2AM,点N在边BC上,且BN=AM,连接AN,MD交于点P,连接OP,则OP的长为 .
18. 如图,正方形ABCD的边长为1,O为对角线BD的中点,点M在边AB上,且BM=2AM,点N在边BC上,且BN=AM,连接AN,MD交于点P,连接OP,则OP的长为 .
三、解答题
-
19. 解方程: .20. 计算: .21. 已知在△ABC中,∠C=90°,AB=4,AC= .
 (1)、求BC;(2)、求sinA.22. 自我省深化课程改革以来,济南市某校开设了:A利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
(1)、求BC;(2)、求sinA.22. 自我省深化课程改革以来,济南市某校开设了:A利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
根据图中信息解决下列问题:
(1)、本次共调查名学生;(2)、补全条形统计图;(3)、扇形统计图中B所对应的扇形的圆心角为度;(4)、根据该校统计的开设数学实践活动课的样本数据,若该校共有1200名学生,请估计该校学生选修A的大约多少人?23. 如图,要用篱笆(虚线部分)围成一个矩形苗圃ABCD,其中两边靠的墙足够长,中间用平行于AB的篱笆EF隔开,已知篱笆的总长度为18米,设矩形苗圃ABCD的一边AB的长为x(m),矩形苗圃ABCD面积为y(). (1)、求y与x的函数关系式;(2)、求所围矩形苗圃ABCD的面积最大值;24. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)、求y与x的函数关系式;(2)、求所围矩形苗圃ABCD的面积最大值;24. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°. (1)、求证:△ABD∽△DCE;(2)、若BD=6,CE=4,求△ABC的边长.25. 直线与反比例函数的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D.
(1)、求证:△ABD∽△DCE;(2)、若BD=6,CE=4,求△ABC的边长.25. 直线与反比例函数的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D. (1)、求直线AB的解析式;(2)、观察图象,当时,直接写出的解集;(3)、若点P是x轴上一动点,当△ADP的面积是6时,求出P点的坐标.26. 如图1,在 中, , , , 、 分别是 、 的中点,连接 ,将 绕点 按逆时针方向旋转,记旋转角为 .
(1)、求直线AB的解析式;(2)、观察图象,当时,直接写出的解集;(3)、若点P是x轴上一动点,当△ADP的面积是6时,求出P点的坐标.26. 如图1,在 中, , , , 、 分别是 、 的中点,连接 ,将 绕点 按逆时针方向旋转,记旋转角为 . (1)、问题发现:
(1)、问题发现:当 时, , 当 时, .
(2)、拓展探究:①当 时, 的值有无变化?请仅就图2的情况给出证明.
②当 为直角三角形时,直接写出线段 的长.
27. 如图,抛物线与x轴交于点A(-1,0)和B(3,0),与y轴交于点C. (1)、求抛物线的表达式;(2)、如图1,若点M为直线BC上方抛物线一动点(与点B、C不重合),做MN平行于y轴,交直线BC于点N,当线段MN的长最大时,请求出点M的坐标;(3)、如图2,若P为抛物线的顶点,动点Q在抛物线上,当时,请求出点Q的坐标.
(1)、求抛物线的表达式;(2)、如图1,若点M为直线BC上方抛物线一动点(与点B、C不重合),做MN平行于y轴,交直线BC于点N,当线段MN的长最大时,请求出点M的坐标;(3)、如图2,若P为抛物线的顶点,动点Q在抛物线上,当时,请求出点Q的坐标.