山东省东营市广饶县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的几何体，上下部分均为圆柱体，其左视图是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y＝（x﹣1）²﹣3的顶点坐标是（）

A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（﹣1，﹣3）

查看试题解析
3. 如图，在⊙O中，A，B，D为⊙O上的点，∠AOB＝52°，则∠ADB的度数是（）

A、104° B、52° C、38° D、26°

查看试题解析
4. 不透明的袋子中装有两个小球，上面分别写着“1”，“-1”除数字外两个小球无其他差别从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为0的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
5. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 $P$ （kPa）是气体体积 $V$ （ $m^{3}$ ）的反比例函数，其图象如图所示，当气体体积为 $1 m^{3}$ 时，气压为（）kPa.

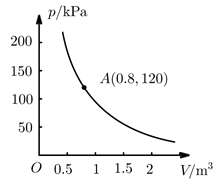A、150 B、120 C、96 D、84

查看试题解析
6. “圆材埋壁”是我国古代数学名著《章算术》中的一个问题：“今有圆材埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺问：径几何？”转化为数学语言：如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为 $E$ ， $C E = 1$ 寸， $A B = 10$ 寸，直径 $C D$ 的长是（）

A、13寸 B、26寸 C、28寸 D、30寸

查看试题解析
7. 用长为6m的铝合金型材做一个形状如图所示的矩形窗框，要使做成的窗框的透光面积最大，则该窗的长，宽应分别做成（）

A、1.5m，1m B、1m，0.5m C、2m，1m D、2m，0.5m

查看试题解析
8. 一个三棱柱的三视图如图所示，其中俯视图为等边三角形，则其表面积为（）

A、 $12 + 2 \sqrt{3}$ B、 $18 + \sqrt{3}$ C、 $18 + 2 \sqrt{3}$ D、 $12 + 4 \sqrt{3}$

查看试题解析
9. 如图，在边长为 $1$ 的小正方形网格中，点 $A ， B ， C ， D$ 都在这些小正方形的顶点上， $A B ， C D$ 相交于点 $O$ ，则 $c o s ∠ B O D =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则下列结论中不正确的有（）个.
①abc＞0；②2a+b＝0；③9a+3b+c＜0；④4ac﹣b²＜0；⑤a+b≥m（am+b）（m为任意实数）.

A、3 B、2 C、1 D、0

查看试题解析

二、填空题

11. 已知α是锐角，2sinα- $\sqrt{2}$ =0，则α=.

查看试题解析
12. 已知点 $P (- 3 ， 2)$ ，点 $Q (2 ， a)$ 都在反比例函数 $y = \frac{k}{x} (x \neq 0)$ 的图象上，过点 $Q$ 分别作两坐标轴的垂线，两垂线与两坐标轴围成的矩形面积为.

查看试题解析
13. 如图，大楼AD高30m，远处有一塔BC，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D测得塔顶的仰角为30°，则塔高BC为m．

查看试题解析
14. 如图是一个地铁站入口的双翼闸机．它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为cm．

查看试题解析
15. 圆锥的侧面展开图的面积是15πcm² ，母线长为5cm，则圆锥的底面半径长为cm．

查看试题解析
16. 某架飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数解析式是y＝60t－ $\frac{3}{2}$ t² ，这架飞机着陆后滑行最后150m所用的时间是s.

查看试题解析
17. 如图，圆内接四边形ABCD，两组对边的延长线分别相交于点E、F，且∠E=40°，∠F=60°，则∠A= °

查看试题解析
18. 在测量时，为了确定被测对象的最佳近似值，经常要对同一对象测量若干次，得到测量结果分别为 $x_{1}$ ， $x_{2}$ ， ……， $x_{n}$ ，然后选取与各测量结果的差的平方和为最小的数作为最佳近似值．即如果设这组测量结果的最佳近似值为 $t_{0}$ ，则 $t_{0}$ 需要使得函数 $y = {(x -_{x})}^{2} + {(x -_{x})}^{2} + \cdot \cdot \cdot + {(x -_{x})}^{2}$ 达到最小值．科研小组利用这种方法来分析麦穗的长度．

(1)、如果在测量了3个麦穗长度之后，得到的数据（单位：cm）是 $x_{1} = 6.2$ ， $x_{2} = 6.0$ ， $x_{3} = 5.8$ ，则按上述方法，可以得到这组数据的最佳近似值为．

(2)、科研小组在（1）的基础上又测量了6个麦穗长度．按上述方法得到这6个数据的最佳近似值为6.3，如果将两组测量的结果合并，则按上述方法计算这9个数据的最佳近似值为．

查看试题解析

三、解答题

19.

(1)、计算： $2 c o s 6 0^{°} - 4 s i n^{2} 4 5^{°} + 3 \sqrt{3} t a n 3 0^{°}$

(2)、如图，已知△ABC中，AB=BC=5， $t a n ∠ A B C = \frac{3}{4}$ ，求边AC的长．

查看试题解析
20. 小明和小亮都想去观看“垃圾分类”宣传演出，但只有一张入场券，于是他们设计了一个“配紫色”游戏： $A$ ， $B$ 是两个可以自由转动的转盘，每个转盘都被分成面积相等的几个扇形．同时转动两个转盘，如果其中一个转盘转出了红色，另一个转盘转出了蓝色，那么可以配成紫色．若配成紫色，则小明去观看，否则小亮去观看．

(1)、转动转盘 $B$ 一次，转出蓝色的概率是；

(2)、这个游戏对双方公平吗？请说明理由（用树状图或列表法）．

查看试题解析
21.
如图，身高1.6米的小明从距路灯的底部（点O）20米的点A沿AO方向行走14米到点C处，小明在A处，头顶B在路灯投影下形成的影子在M处．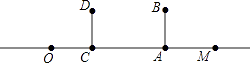

(1)、已知灯杆垂直于路面，试标出路灯P的位置和小明在C处，头顶D在路灯投影下形成的影子N的位置．

(2)、若路灯（点P）距地面8米，小明从A到C时，身影的长度是变长了还是变短了？变长或变短了多少米？

查看试题解析
22. 如图，A、B、C是半径为2的⊙O上三点，AB为直径，∠BAC的平分线交圆于点D，过点D作AC的垂线交AC的延长线于点E，延长线ED交AB的延长线于点F．

(1)、求证：直线EF与 $⊙ O$ 相切；

(2)、若 $D F = 4 \sqrt{2}$ ，求 $c o s ∠ E A D$ 的值．

查看试题解析
23. 如图，某货船以20海里时的速度将一批重要物资由A处运往正西方向的B处，经过16小时的航行到达，到达后必须立即卸货，此时接到气象部门通知，一台风中心正以40海里时的速度由A向北偏西60°的方向移动，距台风中心200海里的区域会受到影响．

(1)、B处是否受台风影响?说明理由；

(2)、若受台风影响，受影响的时间有多长?

(3)、为避免受到台风影响，该船应在多少小时内卸完货?（精确到个位， $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于点A（1，5），B（m，1），与x轴、y轴分别交于点C、D，连接OA、OB．

(1)、求反比例函数和一次函数的表达式；

(2)、求△AOB的面积．

查看试题解析
25. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图（1）所示，每千克成本与销售月份之间的关系如图（2）所示.（其中图（1）的图象是直线，图（2）的图象是抛物线，其最低点坐标是（6，1））.

(1)、求每千克蔬菜销售单价y与销售月份x之间的关系式；

(2)、判断哪个月份销售每千克蔬菜的收益最大？并求最大收益；

(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些？

查看试题解析
26. 如图1，抛物线 $y = a x^{2} + b x + 6$ 与 $x$ 轴交于点 $A$ （2，0） $B$ （6，0），与 $y$ 轴交于点 $C$ ，连接 $A C$ ， $B C$ ．

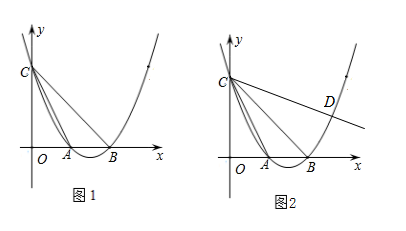(1)、求抛物线的表达式；

(2)、求 $∠ A C B$ 的正切值；

(3)、如图2，过点 $C$ 的直线交抛物线于点 $D$ ，若 $∠ A C D = 45 °$ ，求点 $D$ 的坐标．

查看试题解析