山东省德州市陵城区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组的四条线段a，b，c，d是成比例线段的是（）

A、 $a = 4 ， b = 6 ， c = 5 ， d = 10$ B、 $a = 1 ， b = 2 ， c = 3 ， d = 4$ C、 $a = 2 ， b = 3 ， c = 4 ， d = 5$ D、 $a = 2 ， b = \sqrt{5} ， c = 2 \sqrt{3} ， d = \sqrt{15}$

查看试题解析
2. 下列函数中，y可以看作是x的反比例函数的是（）

A、 $y = \frac{2}{x^{2}}$ B、 $y = \frac{2 - x}{x}$ C、 $y = - \frac{1}{x} + 1$ D、 $y = - 2 x^{- 1}$

查看试题解析
3. 下列说法中正确的是（）

A、“打开电视，正在播放《新闻联播》”是必然事件 B、某次抽奖活动中奖的概率为 $\frac{1}{100}$ ，说明每买100张奖券，一定有一次中奖 C、想了解某市城镇居民人均年收入水平，宜采用抽样调查 D、我区未来三天内肯定下雪

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ （ $a 、 b 、 c$ 为常数，且 $a \neq 0$ ）图像上部分点的横坐标 $x$ 与纵坐标 $y$ 的对应值如下表：
$x$
…
-1
0
1
2
…
$y$
…
0
2
3
3
…
那么，它的对称轴为（）

A、直线 $x = - 1$ B、直线 $x = 0$ C、直线 $x = 1.5$ D、直线 $x = 2$

查看试题解析
5. 在平面直角坐标系中，若点P（x，y）在第四象限，且|x|﹣2＝0，y²﹣9＝0，则点P关于坐标原点对称的点P′的坐标是（）

A、（2，﹣3） B、（﹣3，2） C、（﹣2，3） D、（﹣2，﹣3）

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ B A C = 117 °$ ，将 $△ A B C$ 绕点A按逆时针方向旋转得到 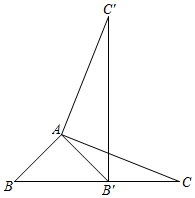$△ A B' C'$ ．若点 $B'$ 刚好落在 $B C$ 边上，且 $A B' = C B'$ ，则 $∠ C'$ 的度数为（）

A、 $42 °$ B、 $21 °$ C、 $63 °$ D、 $30 °$

查看试题解析
7. 如图，直径为10的⊙A经过点 $C$ 和点 $O$ ，点 $B$ 是 $y$ 轴右侧⊙A优弧上一点， $∠ O B C = 30 °$ ，则点 $C$ 的坐标为（）

A、 $(0 ， 10)$ B、 $(0 ， 5)$ C、 $(0 ， 5 \sqrt{3})$ D、 $(0 ， 5 \sqrt{2})$

查看试题解析
8. 如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的位似比为1：2，△EDC的周长为8，则△ABC的周长是（）

A、2 B、4 C、8 D、16

查看试题解析
9. 已知反比例函数y＝ $\frac{b}{x}$ 的图象如图所示，则一次函数y＝cx+a和二次函数y＝ax²﹣bx+c在同一直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，△ABC周长为20cm，BC＝6cm，圆O是△ABC的内切圆，圆O的切线MN与AB、CA相交于点M、N，则△AMN的周长为（）

A、14cm B、8cm C、7cm D、9cm

查看试题解析
11. 下列关于二次函数 $y = - (x - m)^{2} + m^{2} - 2$ （m为常数）的结论：①该函数的图象与函数 $y = - x^{2}$ 的图象形状相同；②该函数的图象一定经过点 $(0 ， - 2)$ ；③当 $x < 0$ 时，y随x的增大而增大；④该函数的图象与函数 $y = 2 x^{2} - 4 m x - 1$ 的图象的对称轴相同．其中所有正确结论的序号是（）

A、①② B、①②④ C、①③④ D、②④

查看试题解析
12. 如图，直线 $y = x + 1$ 与x轴、y轴分别相交于点A、B，过点B作 $B C ⊥ A B$ ，使 $B C = 2 B A$ ，将 $△ A B C$ 绕点O顺时针旋转，每次旋转 $90 °$ ，则第2021次旋转结束时，点C的对应点 $C$ 落在反比例函数 $y = \frac{k}{x}$ 的图象上，则k的值为（）

A、-4 B、4 C、-6 D、6

查看试题解析

二、填空题

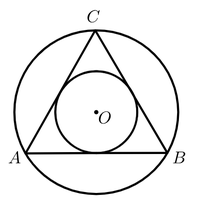
13. 如图，大圆和小圆是等边三角形的外接圆和内切圆，现随机向该图形内掷一枚小针，则针尖落在小圆区域的概率为．

查看试题解析
14. 如图，舞台地面上有一段以点O为圆心的 $\overset{⌢}{A B}$ ，某同学要站在 $\overset{⌢}{A B}$ 的中点C的位置上．于是他想：只要从点O出发，沿着与弦 $A B$ 垂直的方向走到 $\overset{⌢}{A B}$ 上，就能找到 $\overset{⌢}{A B}$ 的中点C，老师肯定了他的想法．这位同学确定点C所用方法的依据是．

查看试题解析
15. 退休的李老师借助自家15米的院墙和总长度为30米的围栏，在院墙外设计一个矩形花圃种植花草．为方便进出，他在如图所示的位置安装了一个1米宽的门，如果设和墙相邻的一边长为x米，花圃面积为y平方米，则y与x之间的函数关系式为．

查看试题解析
16. 如图， $Δ A B C$ 中， $D$ 是 $A C$ 边上一点，且 $∠ A B C = ∠ A D B = 45 °$ ，若 $A D = 2$ ， $C D = 3$ ，则 $A B$ 的长为．

查看试题解析
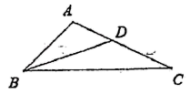17. 如图，点 $P (6 ， 1)$ ，点 $Q (- 2 ， n)$ 都在反比例函数 $y = \frac{k}{x}$ 的图象上．过点P分别向x轴、y轴作垂线，垂足分别为点M，N．连接OP，OQ，PQ．若四边形OMPN的面积记作 $S_{1}$ ， $△ P O Q$ 的面积记作 $S_{2}$ ，则 $S_{1} ： S_{2} =$ ．

查看试题解析
18. 如图，边长为2的正方形ABCD内接于⊙O，点E是 $\overset{⌢}{A B}$ 上一点（不与A、B重合），点F是 $\overset{⌢}{B C}$ 上一点，连接OE，OF，分别与AB，BC交于点G，B，且∠EOF＝90°．有下列结论：① $\overset{⌢}{A E}$ ＝ $\overset{⌢}{B F}$ ；②四边形OGBH的面积随着点E位置的变化而变化；③△GBH周长的最小值为2+ $\sqrt{2}$ ；④若BG＝1﹣ $\frac{\sqrt{3}}{3}$ ，则BG，GE， $\overset{⌢}{B E}$ 围成的面积是 $\frac{π}{12} + \frac{\sqrt{3}}{6}$ ，其中正确的是．（把所有正确结论的序号都填上）

查看试题解析

三、解答题

19. 如图，已知线段 $M N = 4$ ，点A在线段 $M N$ 上，且 $A M = 1$ ，点B为线段 $A N$ 上的一个动点．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，旋转角分别为 $α$ 和 $β$ ．若旋转后M、N两点重合成一点C（即构成 $△ A B C$ ），设 $A B = x$ ．

(1)、 $△ A B C$ 的周长为；

(2)、若 $α + β = 270 °$ ，求x的值．

查看试题解析
20. 有三张正面分别写有数字-2，-1，1的卡片，它们的背面完全相同，将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为 $x$ 的值，放回卡片洗匀，再从三张卡片中随机抽取一张，以其正面的数字作为 $y$ 的值，两次结果记为( $x$ ， $y$ )．

(1)、用树状图或列表法表示( $x$ ， $y$ )所有可能出现的结果；

(2)、求使代数式 $x^{2} - 3 x y$ 与 $y^{2} + x y$ 和的值为1的(x，y)出现的概率；

(3)、求在 $y = - \frac{1}{x}$ 图象上的点( $x$ ， $y$ )出现的概率．

查看试题解析
21. 定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．
如图1，∠E是△ABC中∠A的遥望角，如图2，四边形ABCD内接于⊙O， $\overset{⌢}{A D} = \overset{⌢}{B D}$ ，四边形ABCD的外角平分线DF交⊙O于点F，连接BF并延长交CD的延长线于点E．
求证：∠BEC是△ABC中∠BAC的遥望角．

查看试题解析
22. 在平面直角坐标系中，二次函数y＝x²＋bx＋c的图象交x轴于点A（2，0），B（4，0），交y轴于点C．

(1)、求抛物线解析式，并根据该函数图象写出x＜0时y的取值范围；

(2)、将线段OB向右平移m个单位，向上平移n个单位至O′B′（m，n均为正数），若点O′，B′均落在此二次函数图象上，求m，n的值．

查看试题解析
23. 如图

(1)、问题背景：如图（1），已知 $△ A B C ∽ △ A D E$ ，求证： $△ A B D ∽ △ A C E$ ；

(2)、尝试应用：如图（2），在 $△ A B C$ 和 $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $∠ A B C = ∠ A D E = 30 °$ ， $A C$ 与 $D E$ 相交于点F．点D在 $B C$ 边上， $\frac{A D}{B D} = \sqrt{3}$ ，求 $\frac{D F}{C F}$ 的值．

查看试题解析
24. 如图， $A B$ 是⊙ $O$ 的直径，弦 $C D ⊥ A B$ ，垂足为E，弦 $A F$ 与弦 $C D$ 相交于点G，且 $A G = C G$ ，过点C作 $B F$ 的垂线交 $B F$ 的延长线于点H．

(1)、判断 $C H$ 与⊙ $O$ 的位置关系并说明理由；

(2)、若 $F H = 2 ， B F = 4$ ，求弧 $C D$ 的长．

查看试题解析
25. 甲、乙两名实验者在A、B两个实验室进行空调制冷后舒适度测试，两人同时启动空调1小时后，开始记录数据，经过数据分析，甲的舒适指数 $w_{甲}$ 与空调启动时间 $x (x \geq 1)$ 成反比例关系，乙的舒适指数 $w_{乙}$ 与空调启动时间 $x (x \geq 1)$ 的函数关系式为 $w_{乙} = - 2 (x - h)^{2} + k$ ，函数图象如图所示且在2小时，乙的舒适指数最大．

(1)、求m、k；

(2)、当 $w_{乙} = 9 \frac{1}{2}$ 时，求 $w_{乙} - w_{甲}$ 的较大值；

(3)、若规定舒适度小于1时，实验室则不适合人长时间逗留，求至少启动空调多少小时后，两个实验室均不适合人长时间逗留．

查看试题解析

$x$	…	-1	0	1	2	…
$y$	…	0	2	3	3	…