内蒙古自治区包头市2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-02-17 类型：期末考试
一、单选题
-
1. 若关于x的方程x2＝2x＋a有一个根为－1，则a的值为（ ）A、3 B、1 C、0 D、22. 下列立体图形如图放置，其中同一几何体的左视图与主视图不同的是（ ）A、
B、
C、
D、
3.如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于点A，C，E，B，D，F，若AC=4，CE=6，BD=3，则DF的值是（ ）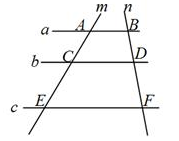
A、4 B、4.5 C、5 D、5.54. 如图，在平面直角坐标系中，△OAB的顶点O在坐标原点，顶点A，B的坐标分别为（－2，－1），（－1.5，0）．△OCD与△OAB位似，位似中心是原点O，若点D的坐标为（4.5，0），则点C的坐标为（ ）
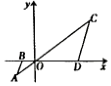A、（6，3） B、（－6，－3） C、（4，2） D、（－4，－2）5. 小亮有两件上衣，分别为蓝色和白色，有两条裤子，分别为黑色和白色，他随机拿出一件上衣和一条裤子穿上，恰好是白色上衣和白色裤子的概率是（ ）A、 B、 C、 D、6. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC＝10cm，接着活动学具成为图2所示正方形，则图2中对角线AC的长为（ ）
A、10cm B、20cm C、30cm D、cm7. 要组织一次篮球邀请赛，参赛的每两个队之间都要比赛一场，赛程共7天，每天3场比赛．设比赛组织者邀请x个队参赛，则根据题意所列方程正确的是（ ）A、x（x＋1）＝21 B、x（x－1）＝21 C、x（x＋1）＝21 D、x（x－1）＝218. 如图，将△ABC沿BC边上的中线AD所在直线向下平移到△的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若A＝1，则'D等于（ ）
A、4 B、3 C、2 D、1.59. 如图，有一路灯杆AP，路灯P距地面4.8m，身高1.6m的小明站在距A点4.8m的点D处，小明的影子为DE，他沿射线DA走2.4m到达点B处，小明的影子为BC，此时小明影子的长度（ ）
A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m10. 如图，在正方形ABCD中，点O是对角线AC，BD的交点，过点O作射线OM，ON分别交BC，CD于点E，F，且∠EOF＝90°，EF，OC交于点G．下列结论：①△COE≌△DOF；②△OGE∽△FGC；③DF2＋BE2＝OG•OC；④正方形ABCD的面积是四边形CEOF面积的4倍．
其中正确的结论是（ ）
A、①②③ B、①②③④ C、①②④ D、③④二、填空题
-
11. 已知a，b，c，d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则d＝cm．12. 口袋中有完全相同的白球若干个，为估计口袋中白球的数量，将8个红球放入口袋中（这些球除颜色外与白球完全相同）．将口袋中的球搅拌均匀后，从中随机摸出一个球，记下颜色后放回口袋中．不断重复这一过程，通过大量的摸球试验，发现摸到红球的频率稳定在0.25左右，由此可以估计口袋中白球的数量为 个．13. 已知点A（－1，y1），B（－2，y2），C（3，y3）在反比例函数的图象上，则y1 ， y2 ， y3的大小关系为 ． （用“＜”连接）14. 将两个直角三角板如图放置，其中AB＝AC，∠BAC＝∠ECD＝90°，∠D＝60°．如果点A是DE的中点，CE与AB交于点F，则∠BFC的度数为 °．
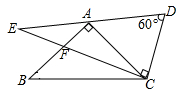15. 如图，△ABC中，AB＝AC，∠B＝72°，∠ACB的角平分线CD交AB于点D．若AC＝2，则CB＝ ．
16. 如果m是方程x2＋2x－3＝0的实根，那么代数式m3－7m的值是 ．17. 如图，双曲线（k≠0）与直线y＝mx（m≠0）交于A（1，2），B两点，将直线AB向下平移n个单位，平移后的直线与双曲线在第一象限的分支交于点C，连接AC并延长交x轴于点D．若点C恰好是线段AD的中点，则n的值为 ．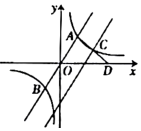
18. 如图，在矩形ABCD中，AB＝6，E是BC的中点，AE与BD交于点F，连接CF．若AE⊥BD，则CF的长为 ．
三、解答题
-
19.(1)、解方程：①x（x＋2）＝3x＋6；
②x2＋8x－9＝0．
(2)、关于x的方程x2－（k－3）x＋1－2k＝0的根的情况是怎样的？请说明理由．20. 两个可以自由转动的转盘A、B都被分成3等份的扇形区域，并在每一小区域内标上数字（如图所示），指针的位置固定．游戏规则：同时转动两个转盘，当转盘停止后，将指针所指两个区域内的数字相乘（若指针落在分割线上，则需重新转动转盘）．
(1)、试用列表或画树状图的方法，求数字之积为3的倍数的概率；(2)、小亮和小芸想用这两个转盘做游戏，他们规定：数字之积为3的倍数时，小亮得2分；数字之积为5的倍数时，小芸得3分．你认为这个游戏对双方公平吗？若公平，请说明理由；若不公平，请修改得分规定，使游戏对双方公平．21. 如图，在4×7的正方形方格纸中（每个小方格的边长均为1）有线段AC和EF，点A，C，E，F均在方格的格点上．
⑴在方格纸中画出一个以AC为对角线的菱形ABCD，点D在直线AC的下方，且点B，D都在方格的格点上；
⑵在方格纸中画出以EF为边的正方形EFGH，且点G，H在方格的格点上；
⑶连接BD交AC于点O，连出△OCE和△CHD，并证明△CHD∽△OCE．
22. 某商场将进货价为30元的台灯以40元售出，一月份售出32台，二、三月份这种台灯销售量连续增长，其中三月份售出50台．(1)、求二月份、三月份两个月这种台灯销售量的月均增长率；(2)、从四月份起商场决定采取降价促销措施，调查发现，在三月份销量的基础上，如果这种台灯的售价每降价2元，那么月销售量增加4台．当每台降价多少元时，四月份销售这种台灯可获利348元？23. 如图，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，边OC在x轴的正半轴上，边OA在y轴的正半轴上，OA＝3，AB＝4，反比例函数（k＞0）的图象与矩形两边AB，BC分别交于点D，点E，且BD＝2AD．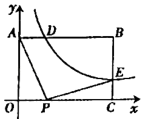
(1)、求点D的坐标和k的值；(2)、连接OD，OE，DE，求△DOE的面积；(3)、若点P是线段OC上的一个动点，是否存在点P，使∠APE＝90°？若存在，求出此时点P的坐标；若不存在，请说明理由．24. 在矩形ABCD的边上取一点E，将沿BE翻折，使点C恰好落在AD边上点F处．(1)、如图，若 ， 求证：
(2)、如图，当时，且时，求BC的长．
(3)、如图，延长EF，与的角平分线交于点M，BM交AD于点N，当时，求的值．