辽宁省大连市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列既是轴对称图形又是中心对称图形的是（）

A、等腰三角形 B、等边三角形 C、平行四边形 D、正方形

查看试题解析
2. 下列事件为必然事件的是（　　）

A、打开电视机，它正在播广告 B、抛掷一枚硬币，一定正面朝上 C、投掷一枚普通的正方体骰子，掷得的点数小于7 D、某彩票的中奖机会是1%，买1张一定不会中奖

查看试题解析
3. 将抛物线y＝x²+1向左平移2个单位长度，再向上平移3个单位长度，则平移后抛物线的顶点坐标为（　　）

A、（﹣2，3） B、（﹣2，﹣4） C、（﹣2，4） D、（2，﹣3）

查看试题解析
4. 如图，点B、D、C是⊙O上的点，∠BDC=130°，则∠BOC是（）

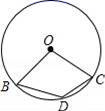A、100° B、110° C、120° D、130°

查看试题解析
5. 不透明的袋子里共装有4个黑球和6个白球，这些球除了颜色不同外，其余都完全相同，随机从袋子中摸出一个球，摸到黑球的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

查看试题解析
6. 如图，把△ABC绕顶点C按顺时针方向旋转得到△A′B′C′，当A′B′⊥AC，∠A＝50°，∠A′CB＝115°时，∠B′CA的度数为（）

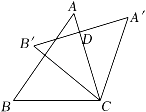A、30° B、35° C、40° D、45°

查看试题解析
7. 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y＝2x²+8x+m上的点，则（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₂＜y₁＜y₃

查看试题解析
8. 如图，下列选项中不能判定△ACD∽△ABC的是（　　）

A、∠ACD＝∠B B、∠ADC＝∠ACB C、AC²＝AD•AB D、BC²＝BD•AB

查看试题解析
9. 电影《长津湖》上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达18亿元，将增长率记作x，则方程可以列为（　　）

A、2+2x+2x²＝18 B、2（1+x）²＝18 C、（1+x）²＝18 D、2+2（1+x）+2（1+x）²＝18

查看试题解析
10. 如图，二次函数y＝ax²+bx+c（a、b、c为常数，且a≠0）的图象与x轴的一个交点坐标为（﹣1，0），对称轴为直线x＝1．下列结论：①x＞0时，y随x的增大而增大；②2a+b＝0；③4a+2b+c＜0；④关于x的方程ax²+bx+c+a＝0有两个不相等的实数根．其中，所有正确结论的序号为（）

A、②③ B、②④ C、①②③ D、②③④

查看试题解析

二、填空题

11. 若关于x的方程 $x^{2} - k x - 12 = 0$ 的一个根为3，则另一个根为．

查看试题解析
12. 抛物线 $y = x^{2} + 1$ 与y轴的交点为．

查看试题解析
13. 如图，已知l₁∥l₂∥l₃ ，直线AB分别交l₁、l₂、l₃于A、M、B，直线CD分别交l₁、l₂、l₃于C、N、D，AM＝4，MB＝6，CD＝9，那么ND＝．

查看试题解析
14. 《算学宝鉴》全称《新集通证古今算学宝鉴》，王文素著,完成于明嘉靖三年,全书12本42卷,近50万字,代表了我国明代数学的最高水平.《算学宝鉴》中记载的用导数解高次方程的方法堪与牛顿媲美,且早于牛顿140年.《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步,之云阔不及长十二步,问长阔共几何？”
译文：一个矩形田地的面积等于864平方步,且它的宽比长少12步，问长与宽的和是多少步？如果设矩形田地的长为x步，可列方程为．

查看试题解析
15. 若一个扇形的半径为3，圆心角是120°，则它的面积是．

查看试题解析
16. 如图，在 $△$ ABC中，∠C＝90°，AC=1， BC=2 ．过B 点作射线BD⊥AB，P是BC上一动点，连接AP，作PQ⊥AP，交射线BD于Q，设AP为x， PQ为y，则y与x的函数关系式为．

查看试题解析

三、解答题

17. 解下列方程：

(1)、x²+2x﹣4＝0（配方法）；

(2)、3x²﹣6x﹣2＝0（公式法）．

查看试题解析
18. 在平面直角坐标系中，已知抛物线y＝x²+bx+c的对称轴为x＝2，且其顶点在直线y＝﹣2x+2上．

(1)、直接写出抛物线的顶点坐标；

(2)、求抛物线的解析式．

查看试题解析
19. 如图，在△ABC中，点D在BC边上，点E在AC边上，且AD＝AB，∠DEC＝∠ADB．

(1)、求证：△AED∽△ADC；

(2)、若AE＝1，EC＝3，求AB的长．

查看试题解析
20. 为庆祝中国共产党建党100周年，某校加强了学生对党史知识的学习，并组织学生参加《党史知识》测试（满分100分）．为了解学生对党史知识的掌握程度，从七、八年级中各随机抽取10名学生的测试成绩，进行统计、分析，过程如下：
收集数据：
七年级：86 88 95 90 100 95 95 99 93 100
八年级：100 98 98 89 87 98 95 90 90 89
整理数据：
成绩x（分）
年级
85＜x≤90
90＜x≤95
95＜x≤100
七年级
3
4
3
八年级
5
a
b
分析数据：
统计量
年级
平均数
中位数
众数
七年级
94.1
95
d
八年级
93.4
c
98
应用数据：

(1)、填空： $a =$ ， $b =$ ， $c =$ ， $d =$ ；

(2)、若八年级共有200人参与答卷，请估计八年级测试成绩大于95分的人数；

(3)、从测试成绩优秀的学生中选出5名语言表达能力较强的学生，其中八年级3名，七年级2名.现从这5名学生中随机抽取2名到当地社区担任党史宣讲员．请用画树状图或列表的方法，求恰好抽到同年级学生的概率．

查看试题解析
21. 2021年7日1日建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

查看试题解析
22. 如图，DP是⊙O的切线，D为切点，弦AB $/ /$ DP，连接BO并延长，与⊙O交于点C，与DP交于点E，连接AC并延长，与DP交于点F，连接OD．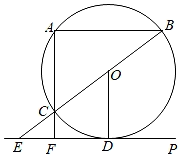

(1)、求证：AF $/ /$ OD；

(2)、若OD＝5，AB＝8，求线段EF的长．

查看试题解析
23. 某商家准备销售一种防护品，进货价格为每件50元，并且每件的售价不低于进货价．经过市场调查，每月的销售量y（件）与每件的售价x（元）之间满足如图所示的函数关系．

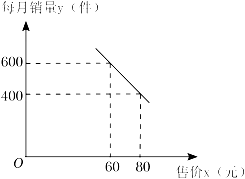(1)、求每月的销售量y（件）与每件的售价x（元）之间的函数关系式；（不必写出自变量的取值范围）

(2)、物价部门规定，该防护品每件的利润不允许高于进货价的30%．设这种防护品每月的总利润为w（元），那么售价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
24. 如图，在平面直角坐标系中，△AOB的边OA在x轴上，OA＝AB，且线段OA的长是方程x²﹣4x﹣5＝0的根，过点B作BE⊥x轴，垂足为E，tan∠BAE＝ $\frac{4}{3}$ ，动点M以每秒1个单位长度的速度，从点A出发，沿线段AB向点B运动，到达点B停止．过点M作x轴的垂线，垂足为D，以MD为边作正方形MDCF，点C在线段OA上，设正方形MDCF与△AOB重叠部分的面积为S，点M的运动时间为t（t＞0）秒．

(1)、求点B的坐标；

(2)、求S关于t的函数关系式，并写出自变量t的取值范围；

查看试题解析
25. 在△ABC中，D为AC上一点，且AC＝kAD，E是BC上一点，BD于AE相交于点O，若∠AOB+∠BAC＝180°．

(1)、如图1，若∠BAC＝120°，AB＝AC．
①找出与∠ABD相等的角，并证明；
②求 $\frac{B D}{A E}$ 的值．

(2)、如图2，若BE＝2CE，求 $\frac{A O}{A B}$ 的值．

查看试题解析
26. 在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ （a，b是常数， $a > 0$ ）与x轴交于A、B两点，与y轴交于点C，对称轴为直线 $x = 1$ ．

(1)、填空： $b =$ （用含a的代数式表示）；

(2)、当 $- 1 \leq x \leq 0$ 时，抛物线上的点到x轴的最大距离为5，求a的值；

(3)、若点A的坐标为 $(- 1 ， 0)$ ，点E的坐标为 $(x ， 0)$ （其中 $x \geq 0$ ），点Q为抛物线上一动点，是否存在以 $C Q$ 为斜边的等腰直角三角形 $C E Q$ ？若存在，求出点E的坐标；若不存在，请说明理由．

查看试题解析