江西省宜春市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件是随机事件的是（）

A、离离原上草，一岁一枯荣 B、太阳每天从东方升起 C、打开电视，正在播放新闻 D、钝角三角形的内角和大于180°

查看试题解析
2. 下列说法正确的是（）

A、三点确定一个圆 B、任何三角形有且只有一个内切圆 C、相等的圆心角所对的弧相等 D、正多边形一定是中心对称图形

查看试题解析
3. 如图，正六边形ABCDEF的半径 $O A = 2$ ，则点B的坐标为（）

A、 $(- \sqrt{3} ， 1)$ B、 $(- 1 ， \sqrt{3})$ C、 $(- 2 ， - \sqrt{3})$ D、 $(- \sqrt{3} ， 2)$

查看试题解析
4. 如图，AE是四边形ABCD外接圆 $⊙ O$ 的直径， $A D = C D$ ， $∠ B = 50 °$ ，则 $∠ D A E$ 的度数为（）

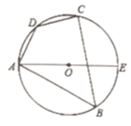A、50° B、55° C、60° D、65°

查看试题解析
5. 如图，将矩形ABCD绕点B按顺时针方向旋转一定角度得到矩形 $A B C D$ ．此时点A的对应点 $A$ 恰好落在对角线AC的中点处．若AB＝3，则点B与点 $D$ 之间的距离为（）

A、3 B、6 C、 $3 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
6. 抛物线y＝ax²+bx+c（a≠0）形状如图，下列结论：①b＞0；②a﹣b+c＝0；③当x＜﹣1或x＞3时，y＞0；④一元二次方程ax²+bx+c+1＝0（a≠0）有两个不相等的实数根．正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

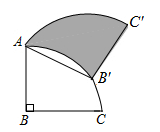
7. 点 $A (1, 5)$ 关于原点对称，得到点 $A'$ ，那么 $A'$ 的坐标是．

查看试题解析
8. 若方程 $x^{2} - 2 x - 3 = 0$ 两根为 $α$ 、 $β$ ，则 $α^{2} + β^{2} =$ ．

查看试题解析
9. 在一个不透明的箱子里装有红色、蓝色、黄色的球共20个，除颜色外，形状、大小、质地等完全相同，小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在20%和35%，则箱子里蓝色球的个数很可能是个.

查看试题解析
10. 圆锥的母线长为 $4 c m$ ，底面半径为 $3 c m$ ，那么它的侧面展开图的圆心角是度.

查看试题解析
11. 如图，将半径为2，圆心角为90°的扇形BAC绕点A逆时针旋转，在旋转过程中，点B落在扇形BAC的弧上的点B' 处，点C的对应点为点C' ，则阴影部分的面积为.

查看试题解析
12. 如图，半圆O的直径 $D E = 12 c m$ ，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ， $B C = 12 c m$ ．半圆O以2cm/s的速度从左向右运动，当圆心O运动到点B时停止，点D、E始终在直线BC上．设运动时间为 $t$ （s），运动开始时，半圆O在 $△ A B C$ 的左侧， $O C = 8 c m$ ．当 $t =$ 时， $R t △ A B C$ 的一边所在直线与半圆O所在的圆相切．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 2 x - 8 = 0$ ；

(2)、关于x的方程 $x^{2} + 4 x + m + 2 = 0$ 有两个相等的实根，求方程的根．

查看试题解析
14. 已知 $P A$ ， $P B$ 是 $⊙ O$ 的两条切线，切点分别是 $A$ 、B，BC垂直 $P A$ 于C，请只用无刻度直尺，按要求画图，保留作图痕迹．

(1)、如图1，连接 $A B$ ，并作出线段 $A B$ 的中点 $D$ ；

(2)、如图2，连接 $O B$ ，过点A作线段AE平行 $O B$ 交PB于点E．

查看试题解析
15. 已知二次函数 $y = x^{2} - k x + k - 5$ ．

(1)、若此二次函数图象的对称轴为 $x = 1$ ，求它的解析式；

(2)、当 $x \leq 1$ 时，y随x增大而减小，求k的取值范围．

查看试题解析
16. 如图，在平面直角坐标系中， $△ A B C$ 的顶点均在格点上，请完成下列问题：

(1)、在图中作出 $△ A B C$ 关于原点O成中心对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、将绕点A逆时针旋转 $90 °$ 得到 $△ A B_{2} C_{2}$ ，请作出 $△ A B_{2} C_{2}$ ，并求出点C到点 $C_{2}$ 的路径长．

查看试题解析
17. 如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2.25m，喷泉水流的运动路线是抛物线，水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3m，以B点为原点，地面水平线和AB所在的直线为x，y轴建立平面直角坐标系，求水流的落地点C到水枪底部B的距离．

查看试题解析
18. 某商店将成本为每件60元的某商品标价100元出售．

(1)、为了促销，该商品经过两次降低后每件售价为81元，若两次降价的百分率相同，求每次降价的百分率；

(2)、经调查，该商品每降价2元，每月可多售出10件，若该商品按原标价出售，每月可销售100件，那么当销售价为多少元时，可以使该商品的月利润最大？最大的月利润是多少？

查看试题解析
19. 如图，AB是⊙O的一条弦，点C是半径OA的中点，过点C作OA的垂线交AB于点E，且与BE的垂直平分线交于点D，连接BD.

(1)、求证：BD是⊙O的切线；

(2)、若⊙O的半径为 $2 \sqrt{3}$ ，CE＝1，试求BD的长.

查看试题解析
20. 我市“垃圾分类”工作越来越好，但还是有不少人缺乏分类意识．某小区分设了四个不同的垃圾分类投放桶，分别为“可回收物”“有害垃圾”厨余垃圾”“其他垃圾”．

(1)、上面图标（不包含文字）是中心对称图形的是（填序号）；

(2)、小明帮助妈妈做家务，拿着一袋厨余垃圾去，因天黑看不清，小明随便扔进了一个垃圾桶，请直接写出小明投放正确的概率；

(3)、然后他又随手将旧报纸和废弃电池扔到其中两类垃圾桶中，那么他恰好符合题意分类的概率是多少？（画树状图或列表求解）．（以上行为均不提倡）

查看试题解析
21. 如图，在矩形ABCD中， $A B = 6 c m$ ， $B C = 12 c m$ ，点P从点A出发沿边AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿边BC以2cm/s的速度向点C移动，当点P运动到点B后，运动停止，设运动时间为x（s）．

(1)、 $B P =$ cm， $C Q =$ cm（用含x的式子表示）；

(2)、若 $P Q = 4 \sqrt{2} c m$ 时，求x的值；

(3)、当x为何值时， $△ D P Q$ 将成为以 $D P$ 为斜边的直角三角形．

查看试题解析
22. 如图

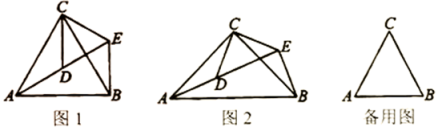(1)、问题发现：如图1， $△ A C B$ 和 $△ D C E$ 均为等边三角形，当 $△ D C E$ 旋转至点A，D，E在同一直线上，连接BE．则：
① $∠ A C B$ 的度数为；
②线段BE，CE与AE之间的数量关系是．

(2)、拓展研究：如图2， $△ A C B$ 和 $△ D C E$ 均为等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ，点A，D，E在同一直线上．若 $C E = \sqrt{2}$ ， $B E = 2$ ，求AB的长度．

(3)、探究发现：图1中的 $△ A C B$ 和 $△ D C E$ ，在 $△ D C E$ 旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索 $∠ A O E$ 的度数，直接写出结果，不必说明理由．

查看试题解析
23. 如图，定义：直线 $l ： y = m x + n (m < 0 ， n > 0)$ 与x轴、y轴分别相交于A，B两点，将 $△ A O B$ 绕着点O逆时针旋转 $90 °$ 得到 $△ C O D$ ，过点A，B，D的抛物线叫做直线l的“纠缠抛物线”，反之，直线叫做抛物线的“纠缠直线”，两线“互为纠缠线”．

(1)、若 $l ： y = - 2 x + 2$ ，则求它的纠缠抛物线的函数解析式；

(2)、判断并说明 $y = - 2 x + 2 k$ 与 $y = - \frac{1}{k} x^{2} - x + 2 k$ 是否“互为纠缠线”；

(3)、在（1）中，P是l的纠缠抛物线在第二象限上的一个动点，求 $△ P C D$ 的最大面积．

查看试题解析