江西省南昌市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 下列四个汽车标志图案中,可以看作是中心对称图形的是 ( )A、
 B、
B、 C、
C、 D、
D、 2. 将点(1,2)绕原点逆时针旋转90°得到的点的坐标是( )A、(﹣1,﹣2) B、(2,﹣1) C、(1,﹣2) D、(﹣2,1)3. 已知关于x的一元二次方程x2﹣3x+1=0有两个不相等的实数根x1 , x2 , 则x12+x22的值是( )A、﹣7 B、7 C、2 D、﹣24. 如图,半径为10的扇形中, , 为弧上一点, , , 垂足分别为 , . 若 , 则图中阴影部分的面积为( )
2. 将点(1,2)绕原点逆时针旋转90°得到的点的坐标是( )A、(﹣1,﹣2) B、(2,﹣1) C、(1,﹣2) D、(﹣2,1)3. 已知关于x的一元二次方程x2﹣3x+1=0有两个不相等的实数根x1 , x2 , 则x12+x22的值是( )A、﹣7 B、7 C、2 D、﹣24. 如图,半径为10的扇形中, , 为弧上一点, , , 垂足分别为 , . 若 , 则图中阴影部分的面积为( )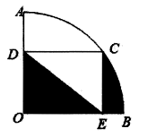 A、 B、 C、 D、5. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为( )米.
A、 B、 C、 D、5. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为( )米. A、8 B、9 C、10 D、116. 如图,AD为的直径, , , 则AC的长度为( )
A、8 B、9 C、10 D、116. 如图,AD为的直径, , , 则AC的长度为( ) A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
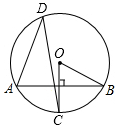
7. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数为奇数的概率是 .8. 如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是
 9. 如图,矩形 中, , , 以点 为中心,将矩形 旋转得到矩形 , 使得点 落在边 上,则 的度数为 .
9. 如图,矩形 中, , , 以点 为中心,将矩形 旋转得到矩形 , 使得点 落在边 上,则 的度数为 .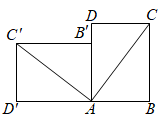 10. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.
10. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.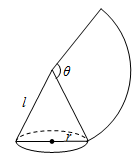 11. 已知抛物线y=ax2﹣4ax+c(a≠0)与x轴交于A、B两点,若点A的坐标为(﹣2,0),则线段AB的长为 .12. 如图,等边 的边长为1,以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画强,交 的延长线于 , 则由弧 , 弧 , 优弧 及线段 围成的图形( )的周长为 .
11. 已知抛物线y=ax2﹣4ax+c(a≠0)与x轴交于A、B两点,若点A的坐标为(﹣2,0),则线段AB的长为 .12. 如图,等边 的边长为1,以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画强,交 的延长线于 , 则由弧 , 弧 , 优弧 及线段 围成的图形( )的周长为 .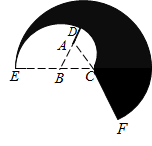
三、解答题
-
13. 解方程:(1)、;(2)、 .14. 已知关于的一元二次方程 . 其中分别为三边的长.(1)、如果是方程的根,试判断的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断的形状,并说明理由.15. 如图,□ABCD 的顶点A、B、D都在⊙O上,请你仅用无刻度的直尺按下列要求画图:
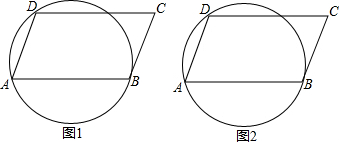 (1)、在图1中,画出一条弦与AD相等;(2)、在图2中,画出一条直线与AB垂直平分.16. 在平面直角坐标系中,已知抛物线 ,经过点 .(1)、求抛物线的函数关系式;(2)、抛物线上有一点 到 轴的距离为 ,求点 坐标.17. 如图,直角坐标系中一条圆弧经过网格点 , , .
(1)、在图1中,画出一条弦与AD相等;(2)、在图2中,画出一条直线与AB垂直平分.16. 在平面直角坐标系中,已知抛物线 ,经过点 .(1)、求抛物线的函数关系式;(2)、抛物线上有一点 到 轴的距离为 ,求点 坐标.17. 如图,直角坐标系中一条圆弧经过网格点 , , .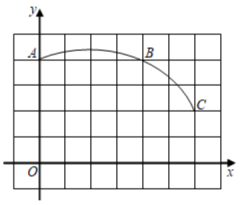 (1)、该圆弧所在圆的圆心坐标为 .(2)、求弧ABC的长.18. 如图,在中,D为边上的一点,过三点的圆O交于点E,已知, .
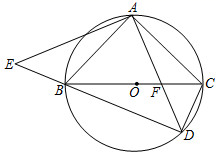
(1)、该圆弧所在圆的圆心坐标为 .(2)、求弧ABC的长.18. 如图,在中,D为边上的一点,过三点的圆O交于点E,已知, .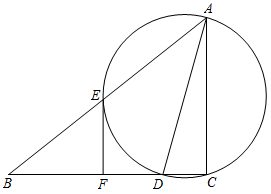 (1)、求证:是圆O的直径;(2)、过点E作于点F,求证:与圆O相切.19. 如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连结并延长OE交圆于点D.
(1)、求证:是圆O的直径;(2)、过点E作于点F,求证:与圆O相切.19. 如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连结并延长OE交圆于点D.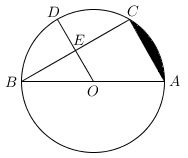 (1)、求证:OD AC.(2)、若DE=2,BE=2 ,求阴影部分的面积.20. 将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌上,随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字.(1)、能组成哪些两位数?(请用树状图表示出来)(2)、恰好是偶数的概率是多少?21. 已知二次函数y=ax2+bx+c的图象分别经过点(0,3)(3,0)(﹣2,﹣5),(1)、求这个二次函数的解析式;(2)、若这个二次函数的图象与x轴交于点C、D(C点在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ABC是等腰三角形,求出点B的坐标.
(1)、求证:OD AC.(2)、若DE=2,BE=2 ,求阴影部分的面积.20. 将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌上,随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字.(1)、能组成哪些两位数?(请用树状图表示出来)(2)、恰好是偶数的概率是多少?21. 已知二次函数y=ax2+bx+c的图象分别经过点(0,3)(3,0)(﹣2,﹣5),(1)、求这个二次函数的解析式;(2)、若这个二次函数的图象与x轴交于点C、D(C点在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ABC是等腰三角形,求出点B的坐标.