江西省九江市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 4 = 0$ 的根为（）

A、 $x = - 2$ B、 $x = 2$ C、 $x = \pm 2$ D、 $x = \pm \sqrt{2}$

查看试题解析
2.
如图，几何体的俯视图是（　　）

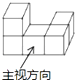A、 B、 C、 D、

查看试题解析
3. 掷一枚质地均匀的硬币10次，下列说法正确的是（）

A、每2次必有一次正面朝上 B、必有5次正面朝上 C、可能有7次正面朝上 D、不可能有10次正面朝上

查看试题解析
4. 已知 $a b = c d$ ，则下列各式不成立的是（）

A、 $\frac{a}{c} = \frac{d}{b}$ B、 $\frac{a}{d} = \frac{c}{b}$ C、 $\frac{a + c}{c} = \frac{d + b}{b}$ D、 $\frac{a + 1}{c + 1} = \frac{d + 1}{b + 1}$

查看试题解析
5. 矩形、菱形、正方形都具有的性质是（）．

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

查看试题解析
6. 已知反比例函数 $y = \frac{1}{x}$ 经过平移后可以得到函数 $y = \frac{1}{x} - 1$ ，关于新函数 $y = \frac{1}{x} - 1$ ，下列结论正确的是（）

A、当 $x > 0$ 时，y随x的增大而增大 B、该函数的图象与y轴有交点 C、该函数图象与x轴的交点为（1，0） D、当 $0 < x \leq \frac{1}{2}$ 时，y的取值范围是 $0 < y \leq 1$

查看试题解析

二、填空题

7. 班主任从甲、乙、丙、丁四位同学中选择一位同学参加学校的演讲比赛．甲同学被选中的概率是．

查看试题解析
8. 反比例函数 $y = \frac{m - 3}{x}$ 的图象在第二、四象限内，那么 $m$ 的取值范围是．

查看试题解析
9. 两个相似多边形的周长比是3：4，其中较小的多边形的面积为 $36 c m^{2}$ ，则较大的多边形的面积为cm² ．

查看试题解析
10. 在平行四边形ABCD中，对角线AC长为8cm， $∠ B A C = 30 °$ ， $A B = 5 c m$ ，则它的面积为cm² ．

查看试题解析
11. 某树主干长出x根枝干，每个枝干又长出x根小分支，若主干、枝干和小分支总数共133根，则主干长出枝干的根数x为．

查看试题解析
12. 如图，在△ABC中，AB=AC=2，∠BAC=90°，O为AC的中点，点P是射线BO上的一个动点，当△ACP为直角三角形时，则BP的长为．

查看试题解析

三、解答题

13. 解方程

(1)、 $x^{2} - 2 x + 1 = 0$

(2)、 $2 x^{2} - 7 x + 3 = 0$

查看试题解析
14. 某校准备从八年级1班、2班的团员中选取两名同学作为运动会的志愿者，已知1班有4名团员（其中男生2人，女生2人）.2班有3名团员（其中男生1人，女生2人）．

(1)、如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长，则这名同学是男生的概率为；

(2)、如果分别从1班、2班的团员中随机各选取一人，请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率．

查看试题解析
15. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1）、（2，1）．

(1)、以O点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出△OB'C′；

(2)、B点的对应点B'的坐标是；C点的对应点C′的坐标是．

查看试题解析
16. 某食品包装盒抽象出的几何体的三视图如图所示．（俯视图为等边三角形）

(1)、写出这个几何体的名称；

(2)、若矩形的长为10cm，等边三角形的边长为4cm，求这个几何体的表面积．

查看试题解析
17. 已知关于x的一元二次方程x²−(2m−2)x+(m²−2m)=0．

(1)、请说明该方程实数根的个数情况；

(2)、如果方程的两个实数根为x₁ ， x₂ ，且(x₁+1)⋅(x₂+1)=8，求m的值．

查看试题解析
18. 晚上，小亮在广场乘凉，图中线段 $A B$ 表示站立在广场上的小亮，线段 $P O$ 表示直立在广场上的灯杆，点 $P$ 表示照明灯．

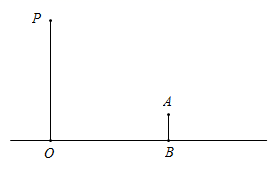(1)、请你在图中画出小亮在照明灯 $P$ 照射下的影子 $B C$ （请保留作图痕迹，并把影子描成粗线）；

(2)、如果小亮的身高 $A B = 1.6 m$ ，测得小亮影长 $B C = 2 m$ ，小亮与灯杆的距离 $B O = 13 m$ ，请求出灯杆的高 $P O$ ．

查看试题解析
19. 如图，在平面直角坐标系中，点O为坐标原点，菱形OABC的顶点A的坐标为（3，4）．

(1)、求过点B的反比例函数 $y = \frac{k}{x}$ 的解析式；

(2)、连接OB，AC交于点H，过点B作 $B D ∥ A C$ 交x轴于点D，求直线BD的解析式．

查看试题解析
20. 某商品每天可售出300件，每件获利2元．为了尽快减少库存，店主决定降价销售．根据经验可知，如果每件降价0.1元，平均每天可多售出20件，店主要想平均每天获利500元，每件商品应降价多少元？

查看试题解析
21. 如图，在四边形ABCD中，∠B=∠C．点E、F、G分别在边AB、BC、CD上，AE=GF=GC．

(1)、求证：四边形AEFG是平行四边形；

(2)、当∠FGC与∠EFB满足怎样的关系时，四边形AEFG是矩形．请说明理由．

查看试题解析
22. 在 $△ A B C$ 中，BC边的长为x，BC边上的高为y， $△ A B C$ 的面积为2

(1)、求y关于x的函数关系式，并说明x的取值范围；

(2)、在平面直角坐标系中画出该函数图象；

(3)、若直线 $y = - x + m$ 与上述函数图象交于点 $P (x_{1} ， y_{1})$ 和点 $Q (x_{2} ， y_{2})$ ，则下面四个结论中，① $x_{1} y_{1} = x_{2} y_{2}$ ；② $x_{1} + y_{1} = x_{2} + y_{2}$ ；③点P，Q关于原点成中心对称；④点P，Q关于直线 $y = x$ 成轴对称，正确的是（直接填序号）．

查看试题解析
23. 如图

(1)、回归教材：北师大七年级下册P44，如图1所示，点P是直线m外一点， $P O ⊥ m$ ，点O是垂足，点A、B、C在直线m上，比较线段PO，PA，PB，PC的长短，你发现了什么？
最短线段是，于是，小明这样总结：直线外一点与直线上各点连接的所有线段中，．

(2)、小试牛刀：如图2所示， $R t △ A B C$ 中， $A B = c$ ， $A C = b$ ， $B C = a$ ．则点P为AB边上一动点，则CP的最小值为．

(3)、尝试应用：如图3所示 $△ A B C$ 是边长为4的等边三角形，其中点P为高AD上的一个动点，连接BP，将BP绕点B顺时针旋转60°得到BE，连接PE、DE、CE．
①请直接写出DE的最小值．
②在①的条件下求 $△ B P E$ 的面积．

(4)、拓展提高：如图4， $R t △ B E F$ 顶点F在矩形ABCD的对角线AC上运动，连接AE． $∠ E B F = ∠ A C D$ ． $A B = 3$ ， $B C = 4$ ，请求出AE的最小值．

查看试题解析