江西省赣州市章贡区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 下面四个图形中,既是轴对称图形也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、若AC、BD为菱形ABCD的对角线,则的概率为1 C、概率很小的事件不可能发生 D、通过少量重复试验,可以用频率估计概率3. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( )
2. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、若AC、BD为菱形ABCD的对角线,则的概率为1 C、概率很小的事件不可能发生 D、通过少量重复试验,可以用频率估计概率3. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( )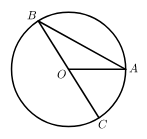 A、 B、 C、 D、4. 如图,在 中, , .将 绕点 逆时针方向旋转 , 得到 , 连接 .则线段 的长为( )
A、 B、 C、 D、4. 如图,在 中, , .将 绕点 逆时针方向旋转 , 得到 , 连接 .则线段 的长为( )
A、1 B、 C、 D、5. 如图,小正方形的边长均为 ,则 、 、 、 四个选项中的三角形(阴影部分)与 相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为( )
6. 若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为( )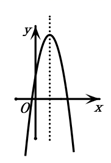 A、
A、 B、
B、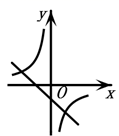 C、
C、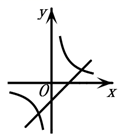 D、
D、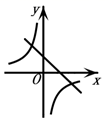
二、填空题
-
7. 的根为 .8. 把抛物线 向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .9. 如图,已知每个小方格的边长均为1,则 与 的周长比为 .
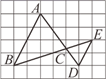 10. 如图,中, , , , 将绕原点O顺时针旋转90°,则旋转后点A的对应点的坐标是 .
10. 如图,中, , , , 将绕原点O顺时针旋转90°,则旋转后点A的对应点的坐标是 . 11. 点(a﹣1,y1)、(a+1,y2)在反比例函数y= (k<0)的图象上,若y1>y2 , 则a的取值范围是 .
11. 点(a﹣1,y1)、(a+1,y2)在反比例函数y= (k<0)的图象上,若y1>y2 , 则a的取值范围是 .
12. 如图,在中,AD为直径,弦于点H,连接OB.已知 , . 动点E从点O出发,在直径AD上沿路线以1cm/s的速度做匀速往返运动,运动时间为 . 当时,的值为 .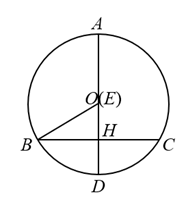
三、解答题
-
13.(1)、解方程:(2)、我国古代数学专著《九章算术》中记载:“今有宛田,下周三十步,径十六步,问为田几何?”注释:宛田是指扇形形状的田,下周是指弧长,径是指扇形所在圆的直径.求这口宛田的面积.14. 已知关于x的一元二次方程x2-4x+m=0.(1)、若方程有实数根,求实数m的取值范围;(2)、若方程两实数根为x1 , x2 , 且满足5x1+2x2=2,求实数m的值.15. 如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.
 (1)、若BC是圆的直径,画出平行四边形ABCD的边CD上的高;(2)、若CD与圆相切,画出平行四边形ABCD的边BC上的高AE.16. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.17. 如图,一次函数 的图象与 轴、 轴分别交于点 , ,与反比例函数 ( )的图象交于点 , .
(1)、若BC是圆的直径,画出平行四边形ABCD的边CD上的高;(2)、若CD与圆相切,画出平行四边形ABCD的边BC上的高AE.16. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.17. 如图,一次函数 的图象与 轴、 轴分别交于点 , ,与反比例函数 ( )的图象交于点 , .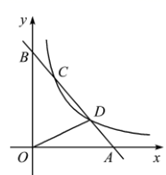 (1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.18. 我们定义:如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.(1)、请说明方程是倍根方程;(2)、若是倍根方程,则 , 具有怎样的关系?(3)、若一元二次方程是倍根方程,则 , , 的等量关系是(直接写出结果)19. 在中, , , 点E在射线CB上运动.连接AE,将线段AE绕点E顺时针旋转90°得到EF,连接CF.
(1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.18. 我们定义:如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.(1)、请说明方程是倍根方程;(2)、若是倍根方程,则 , 具有怎样的关系?(3)、若一元二次方程是倍根方程,则 , , 的等量关系是(直接写出结果)19. 在中, , , 点E在射线CB上运动.连接AE,将线段AE绕点E顺时针旋转90°得到EF,连接CF. (1)、如图1,点E在点B的左侧运动.
(1)、如图1,点E在点B的左侧运动.①当 , 时,则°;
②猜想线段CA,CF与CE之间的数量关系为 .
(2)、如图2,点E在线段CB上运动时,第(1)问中线段CA,CF与CE之间的数量关系是否仍然成立?如果成立,请说明理由;如果不成立,请求出它们之间新的数量关系.20. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第天(为整数)的售价、销量及储存和损耗费用的相关信息如表所示.时间(天)
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
储存和损耗费用(元)
已知该种水果的进价为4.1元/斤,设销售该水果第(天)的利润为(元),求与()之间的函数解析式,并求出第几天时销售利润最大.
21.(1)、探究新知:如图1,已知 与 的面积相等,试判断AB与CD的位置关系,并说明理由.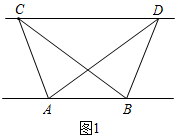 (2)、结论应用:如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N 作 轴,垂足分别为E,F.试证明: .
(2)、结论应用:如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N 作 轴,垂足分别为E,F.试证明: . (3)、拓展延伸:若(2)中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示,MN与x轴、y轴分别交于点A、点B,若 ,请求AN的长.
(3)、拓展延伸:若(2)中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示,MN与x轴、y轴分别交于点A、点B,若 ,请求AN的长.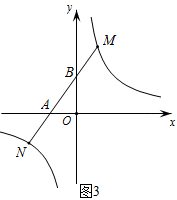 22. 如图,内接于圆O,AB为直径,与点D,E为圆外一点, , 与BC交于点G,与圆O交于点F,连接EC,且 .
22. 如图,内接于圆O,AB为直径,与点D,E为圆外一点, , 与BC交于点G,与圆O交于点F,连接EC,且 . (1)、求证:EC是圆O的切线;(2)、当时,连接CF,
(1)、求证:EC是圆O的切线;(2)、当时,连接CF,①求证:;
②若 , 求线段FG的长.
23. 如图1,在平面直角坐标系中,直线与抛物线相交于A,B两点(点B在第一象限),点C在AB的延长线上.且(n为正整数).过点B,C的抛物线L,其顶点M在x轴上. (1)、求AB的长;(2)、①当时,抛物线L的函数表达式为;
(1)、求AB的长;(2)、①当时,抛物线L的函数表达式为;②当时.求抛物线L的函数表达式;
(3)、如图2,抛物线E:经过B、C两点,顶点为P.且O、B、P三点在同一直线上,①求与n的关系式;
②当时,设四边形PAMC的面积 , 当时,设四边形PAMC的面积(k,t为正整数, , ),若 , 请直接写出值.