黑龙江省哈尔滨市道里区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 下列运算正确的是( )A、(﹣a)2=﹣a2 B、2a2﹣a2=2 C、a2•a=a3 D、(a﹣1)2=a2﹣13. 下列选项中的图形,是轴对称图形、不是中心对称图形的是( )A、
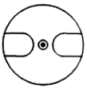 B、
B、 C、
C、 D、
D、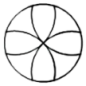 4. 如图是由 个相同的小正方体组成的几何体,则它的俯视图是( )
4. 如图是由 个相同的小正方体组成的几何体,则它的俯视图是( )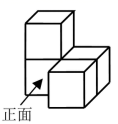 A、
A、 B、
B、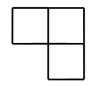 C、
C、 D、
D、 5. 把函数y=(x﹣1)2+2图象向左平移1个单位长度,平移后图象的函数解析式为( )A、y=x2+2 B、y=(x﹣1)2+1 C、y=(x﹣2)2+2 D、y=(x﹣1)2+36. 方程的解为( )A、x=1 B、x=2 C、x=3 D、x=47. 如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )
5. 把函数y=(x﹣1)2+2图象向左平移1个单位长度,平移后图象的函数解析式为( )A、y=x2+2 B、y=(x﹣1)2+1 C、y=(x﹣2)2+2 D、y=(x﹣1)2+36. 方程的解为( )A、x=1 B、x=2 C、x=3 D、x=47. 如图,AB是⊙O的直径,CD是弦,若∠BCD=34°,则∠ABD等于( )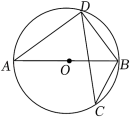 A、66° B、34° C、56° D、68°8. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC= , 将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',连接BB',则BB'的长度是( )
A、66° B、34° C、56° D、68°8. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC= , 将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',连接BB',则BB'的长度是( )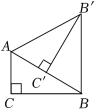 A、1 B、3 C、 D、29. 如图,在 中,点D,E,F分别在AB,AC,BC上, , ,则下列式子一定正确的是( )
A、1 B、3 C、 D、29. 如图,在 中,点D,E,F分别在AB,AC,BC上, , ,则下列式子一定正确的是( )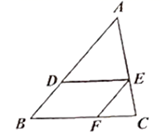 A、 B、 C、 D、10. 为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3 , 打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示,下列说法不正确的是:( )
A、 B、 C、 D、10. 为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3 , 打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示,下列说法不正确的是:( )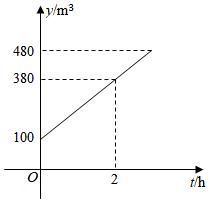 A、该游泳池内开始注水时已经蓄水100m3 B、每小时可注水190m3 C、注水2小时,游泳池的蓄水量为380m3 D、注水2小时,还需注水100m3 , 可将游泳池注满
A、该游泳池内开始注水时已经蓄水100m3 B、每小时可注水190m3 C、注水2小时,游泳池的蓄水量为380m3 D、注水2小时,还需注水100m3 , 可将游泳池注满二、填空题
-
11. 将数13140000用科学记数法表示为 .12. 在函数y=中,自变量x的取值范围是 .13. 已知反比例函数的图象经过点(-2,5),则k= .14. 化简: ﹣3 的结果是 .15. 把多项式a3﹣9ab2分解因式的结果是 .16. 不等式组的解集是 .17. 一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,张兵同学掷一次骰子,骰子向上的一面出现的点数是3的倍数的概率是 .18. 点P为⊙O外一点,直线PO与⊙O的两个公共点为A,B,过点P作⊙O的切线,切点为C,连接AC,若∠CPO=40°,则∠CAB=度.19. 一个扇形的弧长是9πcm,圆心角是108度,则此扇形的半径是 cm.
三、解答题
-
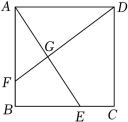
20. 如图,点E在正方形ABCD的边BC上,BE=2CE,点G为垂足,若FG=2,则DG= .
 21. 先化简,再求代数式的值,其中a=3tan30°+1.22. 如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
21. 先化简,再求代数式的值,其中a=3tan30°+1.22. 如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.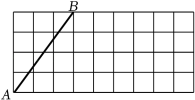
⑴在图中画出等腰△ABC,且△ABC为钝角三角形,点C在小正方形顶点上;
⑵在(1)的条件下确定点C后,再画出矩形BCDE,D,E都在小正方形顶点上,且矩形BCDE的周长为16,直接写出EA的长为 ▲ .
23. 某校为了解学生对生物知识的掌握情况,从中随机抽取了部分学生的成绩作为样本,把成绩按优秀、良好、及格和不及格四个级别进行了统计,抽调的学生成绩为及格的占抽调学生总人数的30%.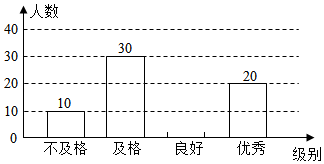 (1)、求一共抽调多少名学生?(2)、请通过计算补全条形统计图;(3)、若该校共有学生2400名,请估计该校学生中有多少人的成绩为不及格?24. 如图,点C,D在AB上, , ∠A=∠B,AE=BF.
(1)、求一共抽调多少名学生?(2)、请通过计算补全条形统计图;(3)、若该校共有学生2400名,请估计该校学生中有多少人的成绩为不及格?24. 如图,点C,D在AB上, , ∠A=∠B,AE=BF.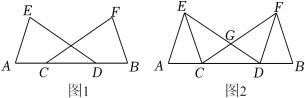 (1)、如图1,求证:DE=FC;(2)、如图2,DE与CF交于点G,连接CE, , 直接写出图中所有面积相等的三角形.25. 某班班主任对在某次考试中取得优异成绩的同学进行表彰.到商场购买了甲、乙两种文具作为奖品,若购买甲种文具12个,乙种文具18个,共花费420元;若购买甲种文具16个,乙种文具14个,共花费460元;(1)、求购买一个甲种、一个乙种文具各需多少元?(2)、班主任决定购买甲、乙两种文具共30个,如果班主任此次购买甲、乙两种文具的总费用不超过500元,求至多需要购买多少个甲种文具?26. 四边形ABCD为矩形,点A,B在⊙O上,连接OC、OD.
(1)、如图1,求证:DE=FC;(2)、如图2,DE与CF交于点G,连接CE, , 直接写出图中所有面积相等的三角形.25. 某班班主任对在某次考试中取得优异成绩的同学进行表彰.到商场购买了甲、乙两种文具作为奖品,若购买甲种文具12个,乙种文具18个,共花费420元;若购买甲种文具16个,乙种文具14个,共花费460元;(1)、求购买一个甲种、一个乙种文具各需多少元?(2)、班主任决定购买甲、乙两种文具共30个,如果班主任此次购买甲、乙两种文具的总费用不超过500元,求至多需要购买多少个甲种文具?26. 四边形ABCD为矩形,点A,B在⊙O上,连接OC、OD.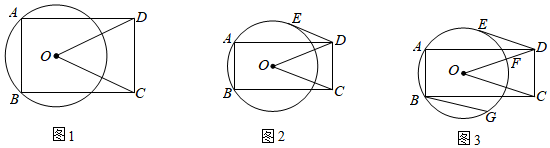 (1)、如图1,求证:OC=OD;(2)、如图2,点E在⊙O上,DE∥OC,求证:DA平分∠EDO;(3)、如图3,在(2)的条件下,DE与⊙O相切,点G在弧BF上,弧FG=弧AE,若BG=3 , DF=2,求AB的长.27. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,点D(4,3)在抛物线上,连接AC,AD,tan∠BAC= .
(1)、如图1,求证:OC=OD;(2)、如图2,点E在⊙O上,DE∥OC,求证:DA平分∠EDO;(3)、如图3,在(2)的条件下,DE与⊙O相切,点G在弧BF上,弧FG=弧AE,若BG=3 , DF=2,求AB的长.27. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,点D(4,3)在抛物线上,连接AC,AD,tan∠BAC= .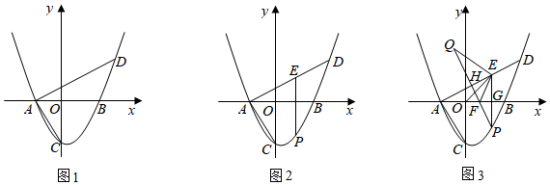 (1)、如图1,求抛物线的解析式;(2)、如图2,点P在抛物线上,点P在第四象限,点P的横坐标为t,过点P作y轴的平行线交AD于点E,设线段PE的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;(3)、如图3,在(2)的条件下,点F在OB上,AF=OB,PE交线段BF于点G,过点F作AE的垂线,点H为垂足,点Q在射线FH上,连接QE,EF,EO,FP,若∠AEO=∠FEO,∠QEF+∠EAC=180°,求点P与点Q的距离.
(1)、如图1,求抛物线的解析式;(2)、如图2,点P在抛物线上,点P在第四象限,点P的横坐标为t,过点P作y轴的平行线交AD于点E,设线段PE的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;(3)、如图3,在(2)的条件下,点F在OB上,AF=OB,PE交线段BF于点G,过点F作AE的垂线,点H为垂足,点Q在射线FH上,连接QE,EF,EO,FP,若∠AEO=∠FEO,∠QEF+∠EAC=180°,求点P与点Q的距离.