河北省石家庄市新乐市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 一元二次方程的根为( ).A、 B、 C、 , D、 ,2. 在一个不透明的袋中装有6个只有颜色不同的球,其中1个红球、2个黄球和3个白球.从袋中任意摸出一个球,是白球的概率为( ).A、 B、 C、 D、3. 如图是某几何体的展开图,该几何体是( )
 A、长方体 B、圆柱 C、圆锥 D、三棱柱4. 的值等于( )A、 B、 C、1 D、25. 如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A、长方体 B、圆柱 C、圆锥 D、三棱柱4. 的值等于( )A、 B、 C、1 D、25. 如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( ) A、60° B、70° C、80° D、90°6. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).
A、60° B、70° C、80° D、90°6. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).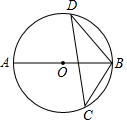 A、60° B、50° C、40° D、20°7. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、60° B、50° C、40° D、20°7. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )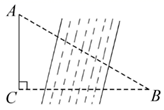 A、 B、 C、 D、9. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,位似比为1:2,设点B的横坐标是a,则点B的对应点B′的横坐标是( ).
A、 B、 C、 D、9. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,位似比为1:2,设点B的横坐标是a,则点B的对应点B′的横坐标是( ).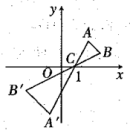 A、 B、 C、 D、10. 将抛物线向下平移两个单位,以下说法不正确的是( )A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变11. 如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )
A、 B、 C、 D、10. 将抛物线向下平移两个单位,以下说法不正确的是( )A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变11. 如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )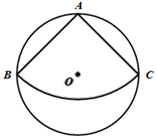 A、 B、 C、 D、112. 有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )A、 B、 C、 D、13. 如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米.
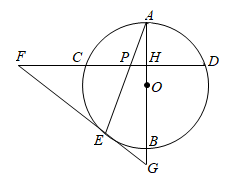
A、 B、 C、 D、112. 有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )A、 B、 C、 D、13. 如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米. A、 B、 C、 D、14. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
A、 B、 C、 D、14. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 时,y的值随x值的增大而增大15. 如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧 ,再分别以E、F为圆心,1为半径作圆弧 、 ,则图中阴影部分的面积为( )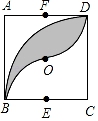 A、π﹣1 B、π﹣2 C、π﹣3 D、4﹣π16. 如图,在纸片中, , 点分别在上,连结 , 将沿翻折,使点A的对应点F落在的延长线上,若平分 , 则的长为( )
A、π﹣1 B、π﹣2 C、π﹣3 D、4﹣π16. 如图,在纸片中, , 点分别在上,连结 , 将沿翻折,使点A的对应点F落在的延长线上,若平分 , 则的长为( )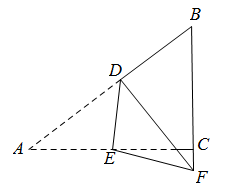 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则这组数据的众数是;平均数是 .
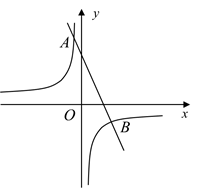
18. 已知关于x的一元二次方程 . 若此方程有两个相等的实数根,则实数k的值为;若此方程有两个实数根,则实数k的取值范围为 .19. 已知:如图,直线与双曲线在第一象限交于点 , 则k的值为;当时, . (填“>”或“<”)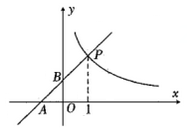
三、解答题
-
20. 2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.(1)、求这两个月参观人数的月平均增长率;(2)、按照这个增长率,预计6月份的参观人数是多少?21. 近5年,我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例,将这3种家电2016~2020年的产量(单位:万台)绘制成如图所示的折线统计图,图中只标注了甲种家电产量的数据.

观察统计图回答下列问题:
(1)、这5年甲种家电产量的中位数为 万台;(2)、若将这5年家电产量按年份绘制成5个扇形统计图,每个统计图只反映该年这3种家电产量占比,其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°,这个扇形统计图对应的年份是 年;(3)、小明认为:某种家电产量的方差越小,说明该家电发展趋势越好.你同意他的观点吗?请结合图中乙、丙两种家电产量变化情况说明理由.22. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质.其研究过程如下: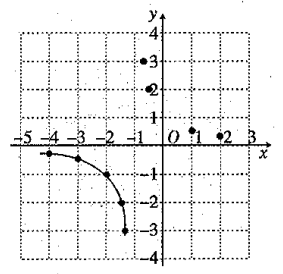 (1)、绘制函数图象.
(1)、绘制函数图象.①列表:下表是x与y的几组对应值,其中 ▲ ;
x
…
-4
-3
-2
0
1
2
…
y
…
-1
-2
-3
3
2
m
…
②描点:根据表中的数值描点 , 请补充描出点;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
(2)、探究函数性质.判断下列说法是否正确(正确的填“√”,不正确的填“×”).
①函数值y随x的增大而减小;
②函数图象关于原点对称;
③函数图象与直线没有交点.
(3)、当时,y随x的增大而减小请你根据图象再写一条此函数的性质: .
23. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G . (1)、求证: BF=CF ;
(1)、求证: BF=CF ;
(2)、若 , ,求FG的长.