广东省中山市2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-02-17 类型：期末考试
一、单选题
-
1. “2022年春节期间，中山市会下雨”这一事件为（ ）A、必然事件 B、不可能事件 C、确定事件 D、随机事件2. 下面四个环境保护图案，属于中心对称图形的是（ ）A、
B、
C、
D、
3. 若一元二次方程的一个根是x=1，则的值是（ ）A、-1 B、0 C、1 D、不能确定4. 在不透明口袋内装有除颜色外完全相同的5个小球，其中红球2个，白球3个．搅拌均匀后，随机抽取一个小球，是红球的概率为（ ）A、 B、 C、 D、5. 抛物线y＝（x﹣1）2＋2的顶点坐标是（ ）A、（2，1） B、（﹣1，2） C、（1，﹣2） D、（1，2）6. 如图，D是等边△ABC外接圆 上的点，且∠CAD=20°，则∠ACD的度数为（ ）
A、20° B、30° C、40° D、45°7. 关于x的一元二次方程x2+3x+4=0的解的情况是（ ）A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、不能确定8. 如图所示，⊙O内切于四边形ABCD，AB＝10，BC＝7，CD＝8，则AD的长度为（ ）
A、8 B、9 C、10 D、119. 如图，在半径为 的圆形纸片中，剪一个圆心角为90°的最大扇形（阴影部分），则这个扇形的面积为 （ ）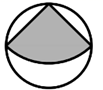
A、π B、 C、2π D、10. 如图，抛物线 与 轴交于 、 两点， 是以点 （0，3）为圆心，2为半径的圆上的动点， 是线段 的中点，连结 .则线段 的最大值是（ ）
A、 B、 C、 D、二、填空题
-
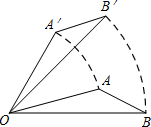
11. 一元二次方程（x+1）2＝4的解为 ．12. 小明和小强玩“石头、剪刀、布”游戏，按照“石头胜剪刀，剪刀胜布，布胜石头，相同算平局”的规则，两人随机出手一次，平局的概率为 ．13. 某试验田种植了杂交水稻，2019年平均亩产800千克，2021年平均亩产1000千克，设此水稻亩产量的平均增长率为x，则可列出的方程是 ．14. 已知⊙A的半径为5，圆心A（4，3），坐标原点O与⊙A的位置关系是 ．15. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是 ．
16. 二次函数y＝ax2＋bx＋4的图象如图所示，则关于x的方程a（x＋1）2＋b（x＋1）＝﹣4的根为 ．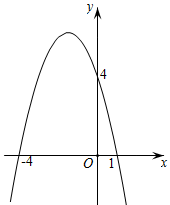
17. 如图所示，半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动．且滚动至扇形处，则顶点O所经过的路线总长是 ．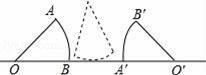
三、解答题
-
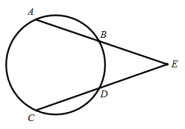
18. 解方程：x（x﹣3）＝x﹣319. 已知抛物线y＝x2+2x-m．(1)、若抛物线与x轴只有一个交点，求此时m的值；(2)、若该抛物线的顶点到x轴的距离为2，求m的值．20. 甲、乙、丙、丁4人聚会，每人带了一件礼物，4件礼物外盒包装完全相同，将4件礼物放在一起．甲先从中随机抽取一件，不放回，乙再从中随机抽取一件，求甲、乙两人抽到的都不是自己带来的礼物的概率．21. 如图，⊙O的弦AB、CD的延长线相交于点E，且EA＝EC．求证：AB＝CD．
22. 如图，在Rt△ABC中，∠C＝90°，将△ABC绕着点B逆时针旋转得到△FBE，点C，A的对应点分别为E，F．点E落在BA上，连接AF．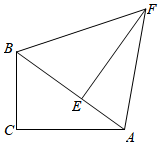
(1)、若∠BAC＝40°，求∠BAF的度数；(2)、若AC＝8，BC＝6，求AF的长．23. 某商场购进一批进货价为16元的日用品，销售一段时间后，为了获得更多的利润，商店决定提高价格．调查发现，若按每件20元的价格销售，每月能卖出360件，若按每件25元的价格销售，每月能卖210件，假定每月销售量y（件）是销售价格x（元/件）的一次函数．(1)、求y与x之间的关系式；(2)、销售价定为多少元时，该商场每月获得利润最大？最大利润是多少？24. 如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD//BM，交AB于点F，且 ， 连接AC，AD，延长AD交BM于点E．
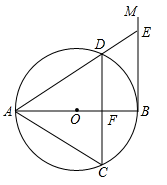(1)、求证：△ACD是等边三角形；(2)、连接OE，若DE＝2，求OE的长．25. 如图，抛物线y＝ax2＋bx﹣3经过A、B、C三点，点A（﹣3，0）、C（1，0），点B在y轴上．点P是直线AB下方的抛物线上一动点（不与A、B重合）．
(1)、求此抛物线的解析式；(2)、过点P作x轴的垂线，垂足为D，交直线AB于点E，动点P在什么位置时，PE最大，求出此时P点的坐标；(3)、点Q是抛物线对称轴上一动点，是否存在点Q，使以点A、B、Q为顶点的三角形为直角三角形？若存在，请求出点Q坐标；若不存在，请说明理由．