广东省阳江市阳东区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，为必然事件的是（）.

A、明天要下雨 B、 $| a | \geq 0$ C、 $- 2 > - 1$ D、打开电视机，它正在播广告

查看试题解析
2. 下列四个标志中.既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线y＝4(2x﹣3)²+3的顶点坐标是（）

A、( $\frac{3}{2}$ ， 3) B、(4，3) C、(3，3) D、(﹣3，3)

查看试题解析
4. 已知反比例函数 $y = \frac{2 - a}{x}$ ，当x＜0时，y随x的增大而增大，则a的值可能是（）

A、3 B、2 C、1 D、-1

查看试题解析
5. 关于x的一元二次方程 $(m - 1) x^{2} + 5 x + m^{2} - 3 m + 2 = 0$ 的常数项是0，则m的值（）

A、1 B、1或2 C、2 D、 $\pm 1$

查看试题解析
6. 如图，⊙O是△ABC的外接圆，∠AOB=60°，AB=AC=2，则弦BC的长为（）

A、 $\sqrt{3}$ B、3 C、2 $\sqrt{3}$ D、4

查看试题解析
7. 已知点A（x﹣2，3）与点B（x+4，y﹣5）关于原点对称，则（）

A、x＝﹣1，y＝2 B、x＝﹣1，y＝8 C、x＝﹣1，y＝﹣2 D、x＝1，y＝8

查看试题解析
8. 如图所示的是反比例函数 $y_{1} = \frac{k}{x} (x > 0)$ 和一次函数 $y_{2} = m x + n$ 的图象，则下列结论正确的是（）

A、反比例函数的解析式是 $y_{1} = \frac{6}{x}$ B、一次函数的解析式为 $y_{2} = - x + 6$ C、当 $x > 6$ 时， $0 < y_{1} < 1$ D、若 $y_{1} < y_{2}$ ，则 $1 < x < 6$

查看试题解析
9. 两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率，绘制出统计图如图所示，则符合这一结果的试验可能是（）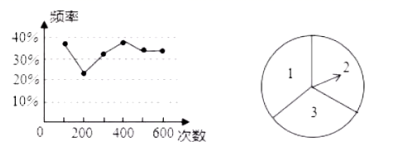

A、抛一枚硬币，正面朝上的概率 B、掷一枚正六面体的骰子，出现 $1$ 点的概率 C、转动如图所示的转盘，转到数字为奇数的概率 D、从装有 $2$ 个红球和 $1$ 个蓝球的口袋中任取一个球恰好是蓝球的概率

查看试题解析
10. 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA₁B₁C₁ ，依此方式，绕点O连续旋转2020次得到正方形OA₂₀₂₀B₂₀₂₀C₂₀₂₀ ，如果点A的坐标为(1，0)，那么点B₂₀₂₀的坐标为（）

A、(﹣1，1) B、( $- \sqrt{2}$ ， 0) C、(﹣1，﹣1) D、(0， $\sqrt{2}$ )

查看试题解析

二、填空题

11. 若关于 $x$ 的一元二次方程 $x^{2} - k x - 2 = 0$ 的一个根为 $x = 1$ ，则这个一元二次方程的另一个根为．

查看试题解析
12. 从﹣1，π， $\sqrt{2}$ ， 1，6中随机取两个数，取到的两个数都是无理数的概率是．

查看试题解析
13. 如图，在平面直角坐标系中，点P（1，1），N（2，0），△MNP和△M₁N₁P₁的顶点都在格点上，△MNP与△M₁N₁P₁是关于某一点中心对称，则对称中心的坐标为.

查看试题解析
14. 如图，将 $△ A B C$ 绕点A逆时针旋转55°得到 $△ A D E$ ，若 $∠ E = 70 °$ 且 $A D ⊥ B C$ 于点F，则 $∠ B A C =$ .

查看试题解析
15. 若一元二次方程x²﹣4x﹣4m＝0有两个不相等的实数根，则反比例函数y $= \frac{m + 2}{x}$ 的图象分别位于第象限．

查看试题解析
16. 设A（﹣2，y₁），B（1，y₂），C（2，y₃）是抛物线y＝﹣（x+1）²+a上的三点，则y₁ ， y₂ ， y₃的大小关系为.

查看试题解析
17. 如图，在平面直角坐标系中，Rt△ABC的顶点A，C的坐标分别是(0，2)，(2，0)，∠ACB＝90°，AC＝2BC．若函数y $= \frac{k}{x}$ （k＞0，x＞0）的图象经过点B，则k的值为．

查看试题解析

三、解答题

18. 解方程：x(2x﹣5)＝2x﹣5．

查看试题解析
19. 如图，一次函数y＝x+1的图像与反比例函数y $= \frac{k}{x}$ 的图像相交，其中一个交点的横坐标是2．求反比例函数的解析式．

查看试题解析
20. 如图，在平面直角坐标系中，A，B，C是⊙M上的三个点，A(0，4)，B(4，4)，C(6，2)，画出⊙M的圆心，并求出圆心M的坐标．

查看试题解析
21. 已知二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象经过A（0，3），B（﹣4，﹣ $\frac{9}{2}$ ）两点．

(1)、求b，c的值．

(2)、二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象与x轴是否有公共点，求公共点的坐标；若没有，请说明情况．

查看试题解析
22. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点分别是A（1，3），B（4，4），C（2，1）．

(1)、①把 $△ A B C$ 向左平移4个单位后得到对应的 $△$ A₁B₁C₁ ，请画出平移后的 $△$ A₁B₁C₁；
②把 $△ A B C$ 绕原点O旋转180°后得到对应的 $△$ A₂B₂C₂ ，请画出旋转后的 $△$ A₂B₂C₂；

(2)、观察图形可知，△A₁B₁C₁与△A₂B₂C₂关于点（，）中心对称．

查看试题解析
23. 将一副扑克牌中点数为“2”、“3”、“4”、“6”的四张牌背面朝上洗匀，先从中抽出1张牌，记录下牌面点数为x，再从余下的3张牌中抽出1张牌，记录下牌面点数为y．设点P的坐标为（x，y）．

(1)、请用表格或树状图列出点P所有可能的坐标．

(2)、求点P在抛物线y＝x²+x上的概率．

查看试题解析
24. 如图，⊙O是直角三角形ABC的外接圆，直径AC＝4，过C点作⊙O的切线，与AB延长线交于点D，M为CD的中点，连接BM，OM，且BC与OM相交于点N．

(1)、求证：BM与⊙O相切；

(2)、当∠BAC＝60°时，求弦AB和弧AB所夹图形的面积；

(3)、在（2）的条件下，在弧AB上取一点F，使∠ABF＝15°，连接OF交弦AB于点H，求FH的长度是多少？

查看试题解析
25. 某科技有限公司成功研制出一种市场急需的电子产品，已于当年投入生产并进行销售，已知生产这种电子产品的成本为4元/件，在销售过程中发现：每年的年销售量y（万件）与销售价格x（元/件）的关系如图，其中AB段为反比例函数图象的一部分，设公司销售这种电子产品的年利润为w（万元）．

(1)、请求出y（万件）与x（元/件）之间的函数关系式；
①求出当4≤x≤8时的函数关系式；
②求出当8＜x≤28时的函数关系式．

(2)、求出这种电子产品的年利润w（万元）与x（元/件）之间的函数关系式；

(3)、求出年利润的最大值．

查看试题解析