广东省深圳市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 深圳湾“春笋”大楼的顶部如图所示，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 若x＝1是关于x的一元二次方程x²+mx﹣3＝0的一个根，则m的值是（）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
3. 如图，已知△ABC∽△DEF，若∠A＝35°，∠B＝65°，则∠F的度数是（）

A、30° B、35° C、80° D、100°

查看试题解析
4. 一元二次方程x²+x﹣1=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
5. 已知菱形的两条对角线的长分别为6cm和8cm，则菱形的面积为（）

A、20 ${cm}^{2}$ B、24 ${cm}^{2}$ C、26 ${cm}^{2}$ D、 $48 {cm}^{2}$

查看试题解析
6. 为庆祝中国共产党成立100周年，某学校开展学习“四史”（《党史》、《新中国史》、《改革开放史》、《社会主义发展史》）交流活动，小亮从这四本书中随机选择1本进行学习心得体会分享，则他恰好选到《新中国史》这本书的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
7. 如图，已知△A′B′C′与△ABC是位似图形，点O是位似中心，若A′是OA的中点，则△A′B'C′与△ABC的面积比是（）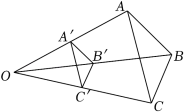

A、1：4 B、1：2 C、2：1 D、4：1

查看试题解析
8. 下列命题中，是真命题的是（）

A、一条线段上只有一个黄金分割点 B、各角分别相等，各边成比例的两个多边形相似 C、两条直线被一组平行线所截，所得的线段成比例 D、若2x＝3y，则 $\frac{x}{y} = \frac{2}{3}$

查看试题解析
9. 文博会期间，某公司调查一种工艺品的销售情况，下面是两位调查员和经理的对话．
小张：该工艺品的进价是每个22元；
小李：当销售价为每个38元时，每天可售出160个；当销售价降低3元时，平均每天将能多售出120个．
经理：为了实现平均每天3640元的销售利润，这种工艺品的销售价应降低多少元？
设这种工艺品的销售价每个应降低x元，由题意可列方程为（）

A、（38﹣x）（160+ $\frac{x}{3}$ ×120）＝3640 B、（38﹣x﹣22）（160+120x）＝3640 C、（38﹣x﹣22）（160+3x×120）＝3640 D、（38﹣x﹣22）（160+ $\frac{x}{3}$ ×120）＝3640

查看试题解析
10. 如图，矩形ABCD中，点E，点F分别是BC，CD的中点，AE交对角线BD于点G，BF交AE于点H．则 $\frac{G H}{H E}$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

11. 若 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a + b}{b}$ = ．

查看试题解析
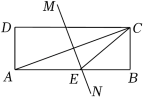
12. 深圳某商场为吸引顾客，设置了一种游戏，其规则如下：在一个不透明的纸箱中装有红球和白球共10个，这些球除颜色外都相同．凡参与游戏的顾客从纸箱中随机摸出一个球，如果摸到红球就可免费得到一个吉祥物，摸到白球没有吉祥物．据统计，参与这种游戏的顾客共有5000人，商场共发放了吉祥物1500个．则该纸箱中红球的数量约有个．

查看试题解析
13. 如图，矩形ABCD中，AC的垂直平分线MN与AB交于点E，连接CE．若∠CAD＝70°，则∠DCE＝°．

查看试题解析
14. 如图，已知一次函数y＝2x+4的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于A，B两点，点B的横坐标是1，过点A作AC⊥y轴于点C，连接BC，则△ABC的面积是．

查看试题解析
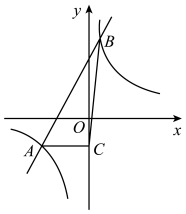15. 如图，已知△ABC与△ADE均是等腰直角三角形，∠BAC＝∠ADE＝90°，AB＝AC＝1，AD＝DE＝ $\sqrt{5}$ ，点D在直线BC上，EA的延长线交直线BC于点F，则FB的长是．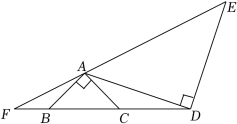

查看试题解析

三、解答题

16. 解方程：x²﹣4x+3=0；

查看试题解析
17. 小明为探究反比例函数y＝ $\frac{k}{x}$ 的性质，他想先画出它的图象，然后再观察、归纳得到．

(1)、他列出y与x的几组对应值如表：
x
…
﹣4
﹣3
﹣2
﹣1
﹣0.5
0.5
1
b
3
4
…
y
…
﹣1
﹣ $\frac{4}{3}$
a
﹣4
﹣8
8
4
2
$\frac{4}{3}$
1
…
表格中，a＝， b＝；

(2)、结合表，在如图所示的平面直角坐标系xOy中，画出当x＞0时的函数y的图象；

(3)、①若（6，m），（10，n）在该函数的图象上，则mn（填“＞”，“＝”或“＜”）；
②若（x₁ ， y₁），（x₂ ， y₂）在该函数的图象上，且x₁＜x₂＜0，则y₁y₂（填“＞”，“＝”或“＜”）．

查看试题解析
18. 深圳某地铁站入口有A，B，C三个安全检查口，假定每位乘客通过任意一个安全检查口的可能性相同．张红与李萍两位同学需要通过该地铁入口乘坐地铁．

(1)、张红选择A安全检查口通过的概率是；

(2)、请用列表或画树状图的方法求出她俩选择相同安全检查口通过的概率．

查看试题解析
19. 如图，点E是矩形ABCD的边BA延长线上一点，连接ED，EC，EC交AD于点G，作CF∥ED交AB于点F，DC＝DE．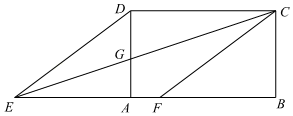

(1)、求证：四边形CDEF是菱形；

(2)、若BC＝3，CD＝5，求AG的长．

查看试题解析
20. 如图①，某校进行校园改造，准备将一块正方形空地划出部分区域栽种鲜花，原空地一边减少了4m，另一边减少了5m，剩余部分面积为650m² ．

(1)、求原正方形空地的边长；

(2)、在实际建造时，从校园美观和实用的角度考虑，按图②的方式进行改造，先在正方形空地一侧建成1m宽的画廊，再在余下地方建成宽度相等的两条小道后，其余地方栽种鲜花，如果栽种鲜花区域的面积为812m² ，求小道的宽度．

查看试题解析
21. 【综合与实践】现实生活中，人们可以借助光源来测量物体的高度．已知榕树CD，FG和灯柱AB如图①所示，在灯柱AB上有一盏路灯P，榕树和灯柱的底端在同一水平线上，两棵榕树在路灯下都有影子，只要测量出其中一些数据，则可求出所需要的数据，具体操作步骤如下：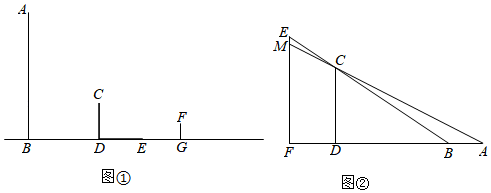
①根据光源确定榕树在地面上的影子；
②测量出相关数据，如高度，影长等；
③利用相似三角形的相关知识，可求出所需要的数据．
根据上述内容，解答下列问题：

(1)、已知榕树CD在路灯下的影子为DE，请画出榕树FG在路灯下的影子GH；

(2)、如图①，若榕树CD的高度为3.6米，其离路灯的距离BD为6米，两棵榕树的影长DE，GH均为4米，两棵树之间的距离DG为6米，求榕树FG的高度；

(3)、无论太阳光还是点光源，其本质与视线问题相同．日常生活中我们也可以直接利用视线解决问题．如图②，建筑物CD高为50米，建筑物MF上有一个广告牌EM，合计总高度EF为70米，两座建筑物之间的直线距离FD为30米．一个观测者（身高不计）先站在A处观测，发现能看见广告牌EM的底端M处，观测者沿着直线AF向前走了5米到B处观测，发现刚好看到广告牌EM的顶端E处．则广告牌EM的高度为米．

查看试题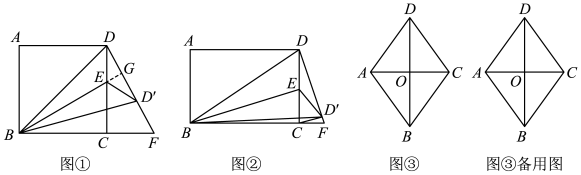解析
22. 如图

(1)、【探究发现】
如图①，已知四边形ABCD是正方形，点E为CD边上一点（不与端点重合），连接BE，作点D关于BE的对称点D'，DD'的延长线与BC的延长线交于点F，连接BD′，D'E．
①小明探究发现：当点E在CD上移动时，△BCE≌△DCF．并给出如下不完整的证明过程，请帮他补充完整．
证明：延长BE交DF于点G．
②进一步探究发现，当点D′与点F重合时，∠CDF＝ ▲ °．

(2)、【类比迁移】
如图②，四边形ABCD为矩形，点E为CD边上一点，连接BE，作点D关于BE的对称点D'，DD′的延长线与BC的延长线交于点F，连接BD'，CD'，D'E．当CD'⊥DF，AB＝2，BC＝3时，求CD'的长；

(3)、【拓展应用】
如图③，已知四边形ABCD为菱形，AD＝ $\sqrt{3}$ ， AC＝2，点F为线段BD上一动点，将线段AD绕点A按顺时针方向旋转，当点D旋转后的对应点E落在菱形的边上（顶点除外）时，如果DF＝EF，请直接写出此时OF的长．

查看试题解析