广东省汕尾市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子是一元二次方程的是（）

A、 $x^{2} - 2 x - 3$ B、 $x^{2} + 1 = y$ C、 $5 - x (x - 1) = 5$ D、 $2 x - 1 = 0$

查看试题解析
2. 下列运动中，属于旋转运动的是（）

A、小明向北走了 4 米 B、一物体从高空坠下 C、电梯从 1 楼到 12 楼 D、小明在荡秋千

查看试题解析
3. 已知⊙O中最长的弦为8cm，则⊙O的半径为（）cm．

A、2 B、4 C、8 D、16

查看试题解析
4. 下列事件中，是必然事件的是（）

A、从一个只有白球的盒子里摸出一个球是白球． B、掷一枚硬币，正面朝上． C、任意买一张电影票座位是3． D、汽车经过红绿灯路口时前方正好是绿灯．

查看试题解析
5. 抛物线y＝2x²﹣1的对称轴是（）

A、直线x＝﹣1 B、直线 $x = \frac{1}{4}$ C、x轴 D、y轴

查看试题解析
6. 方程x²－4＝0的解是（）

A、x＝2 B、x＝－2 C、x＝±2 D、x＝±4

查看试题解析
7. 某商品原价为 200 元，连续两次平均降价的百分率为 a ，连续两次降价后售价为 148 元，下面所列方程正确的是（）

A、200（1 + a）² = 148 B、200（1 - a）² = 148 C、200（1 -2a）² = 148 D、200（1 - a ²）= 148

查看试题解析
8. 一个不透明的口袋中装有10个黑球和若干个白球，小球除颜色外其余均相同，从中随机摸出一球记下颜色，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，由此估计口袋中白球的个数约为（）

A、10个 B、20个 C、30个 D、40个

查看试题解析
9.
如图，AB、AC切⊙O于B、C，AO交⊙O于D，过D作⊙O切线分别交AB、AC于E、F，若OB＝6，AO＝10，则△AEF的周长是（）

A、10 B、12 C、14 D、16

查看试题解析
10. 二次函数 y＝ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c＝0；③若关于 x 的方程ax²+bx+c＝1 有两个根，则这两个根的和为﹣4；④若关于 x 的方程 a（x+5）（x﹣1）=﹣1 有两个根 x₁和 x₂ ，且 x₁＜x₂ ，则﹣5＜x₁＜x₂＜1．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知抛物线 $y = a x^{2} + b x + c$ 的图像与x轴分别交于点 $A (- 2 ， 0)$ ， $B (- 4 ， 0)$ ，则关于x的方程 $a x^{2} + b x + c = 0$ 的根为．

查看试题解析
12. 已知点 P （m + 2， 3）和点 Q （2， n - 4）关于原点对称，则 m + n = ．

查看试题解析
13. 如图，点 A 、 B 、 P 是⊙ O 上的三点，若AOB ＝50°，则APB 的度数为．

查看试题解析
14. 用配方法解方程x²﹣2x﹣5＝0时，将原方程变形为（x﹣a）²＝b的形式为．

查看试题解析
15. 有三张形状、大小、质地都相同的卡片，正面分别标有数字－1，2，3，将它们背面朝上，洗匀后随机抽取一张，不放回，再随机抽取一张，则抽取的两张卡片正面标有数字都是正数的概率为

查看试题解析
16. 如图，AB为半圆的直径，且AB=4，半圆绕点B顺时针旋转45°，点A旋转到A′的位置，则图中阴影部分的面积为．

查看试题解析
17. 如图，在平面直角坐标系中，二次函数 y＝x²﹣2x＋c 的图象与 x 轴交于 A、C 两点，与 y轴交于点 B（0，﹣3），若 P 是 x 轴上一动点，点 D（0，1）在 y 轴上，连接 PD，则 C 点的坐标是， $\sqrt{2}$ PD＋PC 的最小值是．

查看试题解析

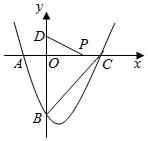
三、解答题

18. 解方程： $x^{2} - 4 x + 3 = 0$ ．

查看试题解析
19. 如图，点A、B、C、D在⊙O上，∠ADC=60°， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ．请判断△ABC的形状，并说明理由．

查看试题解析
20. 如图，在边长为 1 的正方形组成的网格中，△AOB 的顶点均在格点上，点 A，B 的坐标分别是（3，2），（1， 3）)．将△AOB 绕点 O 逆时针旋转90^ 后得到A₁OB₁ ．

(1)、画出A₁OB₁ ，并直接写出点A₁的坐标；

(2)、求旋转过程中点 B 经过的路径长．

查看试题解析
21. 关于x的方程x²﹣2（k﹣1）x+k²＝0有两个实数根x₁ ， x₂ ．

(1)、求k的取值范围；

(2)、请问是否存在实数 k，使得 x₁+x₂＝1﹣x₁x₂ 成立？若存在，求出 k 的值；若不存在，说明理由．

查看试题解析
22.
某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：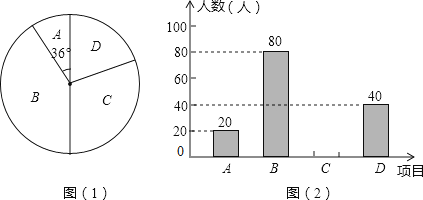

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图（2）补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率.（用树状图或列表法解答）

查看试题解析
23. 一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，该店采取了降价措施．在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

(1)、如果每件盈利30元，平均每天可售出多少件？

(2)、当每件商品降价多少元时，该商店每天销售利润为1050元？

查看试题解析
24. 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．

(1)、求证：CD为⊙O的切线；

(2)、若DC=4，AC=5，求⊙O的直径的AE．

查看试题解析
25. 如图，已知二次函数y=ax²+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．

(1)、求这个二次函数的表达式；

(2)、点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；

(3)、直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．

查看试题解析