广东省梅州市大埔县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. -2021的绝对值是( )A、﹣2021 B、 C、 D、20212. 一组数据:1,2,4,2,2,5,这组数据的众数是( )A、1 B、2 C、4 D、53. 据统计,11月份互联网信息中提及“梅州”一词的次数约为48500000,数据48500000科学记数法表示为( )A、 B、 C、 D、4. 下列美术字中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、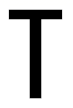 D、
D、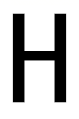 5. 如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1 , 则点B1的坐标是( )
5. 如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1 , 则点B1的坐标是( ) A、(﹣2,3) B、(3,﹣1) C、(﹣3,1) D、(﹣5,2)6. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、57. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、二、三象限 B、一、三象限 C、三、四象限 D、二、四象限8. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
A、(﹣2,3) B、(3,﹣1) C、(﹣3,1) D、(﹣5,2)6. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、57. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、二、三象限 B、一、三象限 C、三、四象限 D、二、四象限8. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )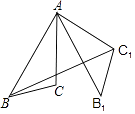 A、6 B、8 C、10 D、129. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、6 B、8 C、10 D、129. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )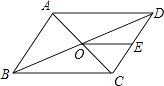 A、15 B、18 C、21 D、2410. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、
A、15 B、18 C、21 D、2410. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 要使二次根式 有意义,则x的取值范围是 .
13. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
14. 有背面完全相同,正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张,现正面朝下放置在桌面上,将其混合后,并从中随机抽取一张,则抽中正面的图形一定是轴对称图形的卡片的概率为.15. 若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 .16. 若x<2,且 ,则x= .17. 如图,矩形 中, , ,对角线 的垂直平分线 交 于点 、交 于点 ,则线段 的长为.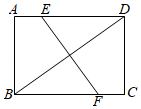
三、解答题
-
18. 计算: .19. 解不等式组: .20. 先化简 ( ),再求值,其中x 2.21. 《国家学生体质健康标准》规定:九年级学生50m测试成绩分为优秀、良好、及格,不及格四个等级,某中学为了了解九年级学生的体质健康状况,对九年级学生进行50m测试,并随机抽取50名男生的成绩进行分析,将成绩分等级制作成不完整的统计表和条形统计图,根据图表信息,解答下列问题:

九年级测试学生人数统计表
等级
人数
优秀
4
良好
a
及格
28
不及格
b
合计
50
(1)、统计表中a的值是 ;(2)、将条形统计图补充完整;(3)、将等级为优秀、良好、及格定为达标,求这50名男生的达标率;(4)、全校九年共有350名男生,估计不及格的男生大约有多少人?22. 如图,点 、 、 、 在同一条直线上, , , .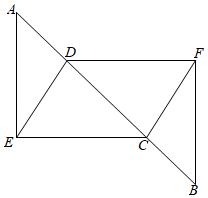
求证:
(1)、 ;(2)、四边形 是平行四边形.23. 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.24. 如图,一次函数的图象与反比例函数的图像相交于、两点.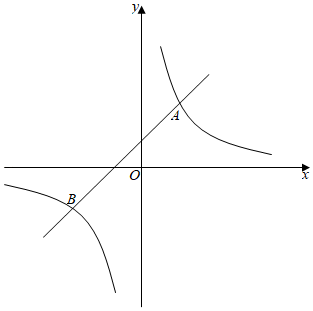 (1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的的取值范围;(3)、若点在线段上,且 , 求点的坐标.25. 如图①,在 中, 于点 , , , 点 是 上一动点(不与点 , 重合),在 内作矩形 ,点 在 上,点 , 在 上,设 ,连接 .
(1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的的取值范围;(3)、若点在线段上,且 , 求点的坐标.25. 如图①,在 中, 于点 , , , 点 是 上一动点(不与点 , 重合),在 内作矩形 ,点 在 上,点 , 在 上,设 ,连接 .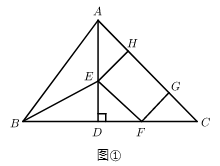
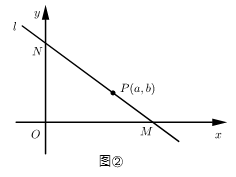 (1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.
(1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.