广东省茂名市高州市2021-2022学年九年级上学期期末联考数学试题(A卷)
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 如图所示的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
2. 若 , 则的值为( )A、 B、 C、 D、
-
3. 如图,下列选项中不能判定△ACD∽△ABC的是( )
 A、= B、= C、∠ACD=∠B D、∠ADC=∠ACB
A、= B、= C、∠ACD=∠B D、∠ADC=∠ACB -
4. 如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分) ,余下部分种植草坪,要使草坪的面积为540平方米,则设道路的宽为xm,根据题意,列方程( ) .
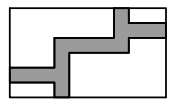 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图,函数 与函数 的图象相交于点 , .若 ,则x的取值范围是( )
 A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或 -
6. 若 ,则代数式 的值( )A、-1 B、3 C、-1或3 D、1或-3
-
7. 有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为( )A、8人 B、9人 C、10人 D、11人
-
8. 如图,已知△ABC和△A′B′C′是以点C为位似中心的位似图形,且△ABC和△A′B′C′的周长之比为1∶2,点C的坐标为(-1,0),若点B的对应点B′的横坐标为5,则点B的横坐标为( )
 A、-5 B、-4 C、 D、-3
A、-5 B、-4 C、 D、-3 -
9. 如图,平行四边形ABCD的边BC上有一动点E,连接DE,以DE为边作矩形DEGF且边FG过点A.在点E从点B移动到点C的过程中,矩形DEGF的面积( )
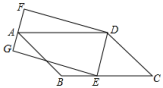 A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变 -
10. 如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是与的角平分线,AE的延长线与DF相交于点G,则下列结论:①;②;③;④ , 其中正确的有( )个
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
11. 若关于x的一元二次方程x2﹣10x+m=0可以通过配方写成(x﹣n)2=0的形式,那么于m+n的值是
-
12. 已知关于x的一元二次方程x2﹣3x+1=0有两个不相等的实数根x1 , x2 , 则x12+x22的值是
-
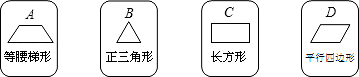
13. 有4张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).将这4张纸牌背面朝上洗匀后先由小明从中任意摸出一张,放回洗匀后再由小敏从中任意摸出一张,则“小明所摸纸牌是中心对称图形,小敏所摸纸牌是轴对称图形”的概率为 .
-
14. 如图,在菱形ABCD中,∠C=60º,E、F分别是AB、AD的中点,若EF=5,则菱形ABCD的周长为 .

-
15. 如图,将放置在的正方形网格中,如果顶点A、B、C均在格点上,那么的正切值为 .

-
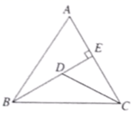
16. 如图, 中, , , 于点 , 是线段 上的一个动点,则 的最小值是.
-
17. 如图,已知△P1OA1 , △P2A1A2 , △P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 .

三、解答题
-
18. 计算:2cos30°+|﹣2|﹣(π﹣2020)0﹣()﹣1 .
-
19. 某几何体的三视图如图所示,已知在△EFG中,FG=18cm,EG=12cm,∠EGF=30°;在矩形ABCD中,AD=16cm.
 (1)、请根据三视图说明这个几何体的形状.(2)、请你求出AB的长;(3)、求出该几何体的体积.
(1)、请根据三视图说明这个几何体的形状.(2)、请你求出AB的长;(3)、求出该几何体的体积. -
20. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
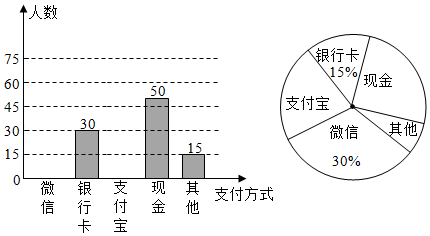 (1)、这次活动共调查了人;(2)、在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(3)、在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
(1)、这次活动共调查了人;(2)、在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(3)、在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率. -
21. 如图,在鉴江的右岸边有一高楼AB,左岸边有一坡度i=1:2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行了20米到达点D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.

-
22. 已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
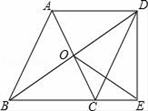 (1)、求证:DE⊥BE;(2)、如果OE⊥CD,求证:BD•CE=CD•DE.
(1)、求证:DE⊥BE;(2)、如果OE⊥CD,求证:BD•CE=CD•DE. -
23. 某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示:
 (1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?
(1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元? -
24. 如图,矩形ABCD中,长AB和宽AD的长度分别是方程的两个根,点E为AD上一个动点,将沿CE折叠得到 , 点D的对应点为F.
 (1)、求AB与AD的长;(2)、当点F恰好落在AB边上时,
(1)、求AB与AD的长;(2)、当点F恰好落在AB边上时,①求DE的长;
②动点M从点F出发沿FC向C点匀速运动,速度为每秒2个单位长度,同时动点N以每秒1个单位长度的速度从C点出发,沿CB匀速向B点运动,当点M到达C点时,两点同时停止运动,设运动时间为t,若以M,N,C为顶点的三角形与相似时,求t的值.
-
25. 如图1,已知点A(a,0),B(0,b),且a、b满足+(a+b+3)2=0,平行四边形ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y=上经过C、D两点.
 (1)、a= , b=;(2)、求反比例函数表达式;(3)、点P在双曲线y=上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,直接写出满足要求的所有点Q的坐标;(4)、以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,直接写出其变化范围;若不改变,请直接写出其值.
(1)、a= , b=;(2)、求反比例函数表达式;(3)、点P在双曲线y=上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,直接写出满足要求的所有点Q的坐标;(4)、以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,直接写出其变化范围;若不改变,请直接写出其值.
