广东省广州市南沙区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 平面直角坐标系内一点（-3，4）关于原点对称点的坐标是（）

A、（3，4） B、（-3，-4） C、（3，-4） D、（4，-3)

查看试题解析
2. 如图，在⊙O中，OC⊥AB，若∠BOC＝40°，则∠OAB等于（）

A、40° B、50° C、80° D、120°

查看试题解析
3. 抛物线y＝﹣2（x﹣3）²﹣4的对称轴是（）

A、直线x＝3 B、直线x＝﹣3 C、直线x＝4 D、直线x＝﹣4

查看试题解析
4. 连续抛掷两次骰子，它们的点都是奇数的概率是（）

A、 $\frac{1}{36}$ B、 $\frac{1}{9}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
5. 如图，在一幅长 $60 c m$ ，宽 $40 c m$ 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是 $2816 c m^{2}$ ，设金色纸边的宽为 $x c m$ ，那么x满足的方程是（）

A、 $(60 + x) (40 + 2 x) = 2816$ B、 $(60 + x) (40 + x) = 2816$ C、 $(60 + 2 x) (40 + x) = 2816$ D、 $(60 + 2 x) (40 + 2 x) = 2816$

查看试题解析
6. 二次函数y＝ax²+bx+c的图象如图所示，则一次函数y＝﹣bx+c的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，正六边形螺帽的边长是4cm，那么这个正六边形半径R和扳手的开口a的值分别是（）

A、2，2 $\sqrt{3}$ B、4，4 $\sqrt{3}$ C、4，2 $\sqrt{3}$ D、4， $\sqrt{3}$

查看试题解析
8. 如图，将△ABC绕点A顺时针旋转α，得到△ADE，若点D恰好在CB的延长线上，则∠CDE等于（）

A、α B、90°+ $\frac{α}{2}$ C、90°﹣ $\frac{α}{2}$ D、180°﹣2α

查看试题解析
9. 定义新运算“a⊗b”：对于任意实数a，b，都有a⊗b＝（a﹣b）²﹣b，其中等式右边是通常的加法、减法和乘法运算，如3⊗2＝（3﹣2）²﹣2＝﹣1．若x⊗k＝0（k为实数）是关于x的方程，且x＝2是这个方程的一个根，则k的值是（）

A、4 B、﹣1或4 C、0或4 D、1或4

查看试题解析
10. 已知平面直角坐标系中有点A（﹣4，﹣4），点B（a，0），二次函数y＝x²+（k﹣3）x﹣2k的图象必过一定点C，则AB+BC的最小值是（）

A、4 $\sqrt{13}$ B、2 $\sqrt{13}$ C、6 $\sqrt{2}$ D、3 $\sqrt{2}$

查看试题解析

二、填空题

11. 若方程mx²+3x-4=3x²是关于x的一元二次方程，则m的取值范围是

查看试题解析
12. 为了估计池塘里有多少条鱼，先从池溏里捕捞100条鱼做上记号，然后放回池塘里去，经过一段时间，待有标记的鱼完全混合于鱼群后，第二次再捕捞300条鱼，若其中有15条有标记，那么估计池塘里大约有鱼条．

查看试题解析
13. 如图，扇形AOB的圆心角为120°，弦AB＝2 $\sqrt{3}$ ，则图中阴影部分的面积是．

查看试题解析
14. 已知⊙O的直径为8cm，如果直线AB上的一点与圆心的距离为4cm，则直线AB与⊙O的位置关系是．

查看试题解析
15. 已知二次函数y＝﹣x²+bx+c与一次函数y＝mx+n的图象相交于点A（﹣2，4）和点B（6，﹣2），则不等式﹣x²+bx+c＞mx+n的解集是．

查看试题解析
16. 如图，已知Rt△ABC中，∠ABC＝90°，∠ACB＝30°，斜边AC＝4，点P是三角形内的一动点，则PA+PB+PC的最小值是．

查看试题解析

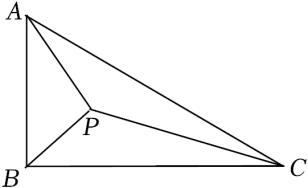
三、解答题

17. 解方程：（x+3）²﹣2x（x+3）＝0．

查看试题解析
18. 如图，四边形ABCD内接于⊙O，E为BC延长线上的一点，点C为 $\overset{⌢}{B D}$ 的中点．若∠DCE＝110°，求∠BAC的度数．

查看试题解析
19. 如图，已知△ABC中，BD是中线．

(1)、尺规作图：作出以D为对称中心，与△BCD成中心对称的△EAD．

(2)、猜想AB+BC与2BD的大小关系，并说明理由．

查看试题解析
20. 如图是一座抛物线形的拱桥，拱桥在竖直平面内，与水平桥相交于A，B两点，拱桥最高点C到AB的距离为9m，AB＝36m，D，E为拱桥底部的两点，DE $∥$ AB．

(1)、以C为原点，以抛物线的对称轴为y轴建立直角坐标系，求出此时抛物线的解析式．（忽略自变量取值范围）

(2)、若DE＝48m，求E点到直线AB的距离．

查看试题解析
21. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4，小明随机从口袋中摸取一个小球，记录摸到小球的标号后放回，再从中摸取一个小球，又放回．小明摸取了60次，结果统计如下：
标号
1
2
3
4
次数
16
14
20
10

(1)、上述试验中，小明摸取到“2”号小球的频率是；小明下一次在袋中摸取小球，摸到“2”号小球的概率是；

(2)、若小明随机从口袋中摸取一个小球，记录摸到小球的标号后放回，再从中摸取一个小球，请用列举法求小明两次摸取到小球的标号相同的概率．

(3)、若小明一次在袋中摸出两个小球，求小明摸出两个小球标号的和为5的概率．

查看试题解析
22. 在平面直角坐标系中，以坐标原点为圆心的⊙O半径为3．

(1)、试判断点A（3，3）与⊙O的位置关系，并加以说明．

(2)、若直线y＝x+b与⊙O相交，求b的取值范围．

(3)、若直线y＝x+3与⊙O相交于点A，B．点P是x轴正半轴上的一个动点，以A，B，P三点为顶点的三角形是等腰三角形，求点P的坐标．

查看试题解析
23. 已知关于x的方程ax²﹣（2a+1）x+a﹣2＝0．

(1)、若方程有两个实数根，求a的取值范围．

(2)、若x＝2是方程的一个根，求另一个根．

(3)、在（1）的条件下，试判断直线y＝（2a﹣3）x﹣a+5能否过点A（﹣1，3），并说明理由．

查看试题解析
24. 已知关于x的一元二次方程﹣ $\frac{1}{2} x^{2}$ +ax+a+3＝0．

(1)、求证：无论a为任何实数，此方程总有两个不相等的实数根；

(2)、如图，若抛物线y＝﹣ $\frac{1}{2} x^{2}$ +ax+a+3与x轴交于点A（﹣2，0）和点B，与y轴交于点C，连结BC，BC与对称轴交于点D．
①求抛物线的解析式及点B的坐标；
②若点P是抛物线上的一点，且点P位于直线BC的上方，连接PC，PD，过点P作PN⊥x轴，交BC于点M，求△PCD的面积的最大值及此时点P的坐标．

查看试题解析
25. 已知：如图①，AD为⊙O的直径，点A为优弧 $\overset{⌢}{B C}$ 的中点，延长BO交AC于点E．

(1)、求证：∠BAC＝2∠ABE；

(2)、若△BCE是等腰三角形时，求∠BCE的度数；

(3)、如图②，若弦BC垂直平分半径OD，连接DE交BC于点F，DF＝a，EF＝k•DF，S_△BEF＝1，M、N、P分别为直线BD、BF、DF上的三个动点，求△MNP周长的最小值．

查看试题解析

标号	1	2	3	4
次数	16	14	20	10