北京市门头沟区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $2 a = 3 b (a b \neq 0)$ ，则下列比例式成立的是（）

A、 $\frac{a}{2} = \frac{3}{b}$ B、 $\frac{a}{3} = \frac{b}{2}$ C、 $\frac{a}{b} = \frac{2}{3}$ D、 $\frac{b}{a} = \frac{3}{2}$

查看试题解析
2. 二次函数 $y = {(x - 3)}^{2} + 1$ 的顶点坐标是（）

A、 $(- 3 ， 1)$ B、 $(3 ， 1)$ C、 $(- 3 ， - 1)$ D、 $(3 ， - 1)$

查看试题解析
3. 已知⊙ $O$ 的半径为 $5$ ，点 $P$ 到圆心 $O$ 的距离为 $8$ ，那么点 $P$ 与⊙ $O$ 的位置关系是（）．

A、点 $P$ 在⊙ $O$ 外 B、点 $P$ 在⊙ $O$ 内 C、点 $P$ 在⊙ $O$ 上 D、无法确定

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $t a n A = 2$ ，则 $s i n A$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
5. 如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（）

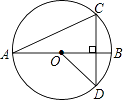A、160° B、150° C、140° D、120°

查看试题解析
6. 如果将抛物线 $y = 2 x^{2}$ 先向左平移2个单位，再向上平移3个单位后得到一条新的抛物线，这条新的抛物线的表达式是（）

A、 $y = 2 {(x - 2)}^{2} + 3$ B、 $y = 2 {(x + 2)}^{2} - 3$ C、 $y = 2 {(x - 2)}^{2} - 3$ D、 $y = 2 {(x + 2)}^{2} + 3$

查看试题解析
7. 如果 $A (1 ， y_{1})$ 与 $B (2 ， y_{2})$ 都在函数 $y = \frac{k - 1}{x}$ 的图象上，且 $y_{1} > y_{2}$ ，那么 $k$ 的取值范围是（）

A、 $k > 1$ B、 $k < 1$ C、 $k \neq 1$ D、任意实数

查看试题解析
8. 如图，抛物线 $y = \frac{1}{4} x^{2} - 4$ 与 $x$ 轴交于 $A$ 、 $B$ 两点， $P$ 是以点 $C$ （0，3）为圆心，2为半径的圆上的动点， $Q$ 是线段 $P A$ 的中点，连结 $O Q$ .则线段 $O Q$ 的最大值是（）

A、 $3$ B、 $\frac{\sqrt{41}}{2}$ C、 $\frac{7}{2}$ D、 $4$

查看试题解析

二、填空题

9. 已知 $\frac{x}{y}$ ＝ $\frac{2}{3}$ ，那么 $\frac{x + y}{x}$ ＝．

查看试题解析
10. 颐和园是我国现存规模最大，保存最完整的古代皇家园林，它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园．该园有一个六角亭，如果它的地基是半径为2米的正六边形，那么这个地基的周长是米．

查看试题解析
11. 如果两个相似三角形的相似比是 $1 ： 3$ ，那么这两个相似三角形的周长比是．

查看试题解析
12. 如图，扇形的圆心角∠AOB=60°，半径为3cm．若点C、D是 $\overset{⌢}{A B}$ 的三等分点，则图中所有阴影部分的面积之和是cm² ．

查看试题解析
13. 把二次函数y=x²﹣2x+3化成y=a（x﹣h）²+k的形式为．

查看试题解析
14. 写出一个图象位于第一，三象限的反比例函数的表达式．

查看试题解析
15. 《九章算术》是我国古代的数学名著，书中有这样的一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”．其意思是：“如图，现有直角三角形，勾（短直角边）长为 8 步，股（长直角边）长为 15 步，问该直角三角形所能容纳的最大圆的直径是多少？”答：该直角三角形所能容纳的最大圆的直径是步．

查看试题解析
16. 函数 $y = \frac{1}{2} x^{2} + \frac{1}{x}$ 的图象如图所示，在下列结论中：①该函数自变量 $x$ 的取值范围是 $x \neq 0$ ；② 该函数有最小值 $\frac{3}{2}$ ；③方程 $\frac{1}{2} x^{2} + \frac{1}{x} = 3$ 有三个根；④如果 $(x_{1} ， y_{1})$ 和 $(x_{2} ， y_{2})$ 是该函数图象上的两个点，当 $x_{1} < x_{2} < 0$ 时一定有 $y_{1} < y_{2}$ ．所有正确结论的序号是．

查看试题解析
17. 已知：如图，在 $△ A B C$ 中，点D在BC上，点E在AC上，DE与AB不平行 $.$ 添加一个条件，使得 $△ C D E$ ∽ $△ C A B$ ，然后再加以证明．

查看试题解析

三、解答题

18. 计算： $2 s i n 60 ° + \sqrt{12} + | - 5 | - {(π - \sqrt{2})}^{0}$ ．

查看试题解析
19. 下面是小明设计的“作等腰三角形外接圆”的尺规作图过程.
已知：如图1，在 $Δ A B C$ 中，AB=AC.
求作：等腰 $Δ A B C$ 的外接圆.
作法：
①如图2，作 $∠ B A C$ 的平分线交BC于D；
②作线段AB的垂直平分线EF；
③EF与AD交于点O；
④以点O为圆心，以OB为半径作圆.
所以， $⊙ O$ 就是所求作的等腰 $Δ A B C$ 的外接圆.
根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留痕迹）；

(2)、完成下面的证明.
$∵$ AB=AC， $∠ B A D = ∠ D A C$ ，
$∴$ .
$∵$ AB的垂直平分线EF与AD交于点O，
$∴$ OA=OB，OB=OC
（填写理由：）
$∴$ OA=OB=OC.

查看试题解析

20. 已知二次函数

y = a x^{2} + b x + c

图象上部分点的横坐标

x

、纵坐标

y

的对应值如下表：

$x$	…	0	1	2	3	4	…
$y$	…	-3	-4	-3	0	5	…

(1)、求该二次函数的表达式；

(2)、直接写出该二次函数图象与

x

轴的交点坐标.

查看试题解析

21. 如图，在Rt△ABC中，∠ACB=90°，CD是边AB上的高．

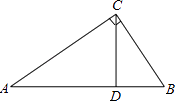(1)、求证：△ABC∽△CBD；

(2)、如果AC=4，BC=3，求BD的长．

查看试题解析
22. 如图，在平面直角坐标系xOy中，一次函数y=﹣2x的图象与反比例函数y= $\frac{k}{x}$ 的图象的一个交点为A（﹣1，n）．

(1)、求反比例函数y= $\frac{k}{x}$ 的解析式；

(2)、若P是坐标轴上一点，且满足PA=OA，直接写出点P的坐标．

查看试题解析
23. “永定楼”是门头沟区的地标性建筑，某数学兴趣小组进行了测量它高度的社会实践活动．如图，他们先在点 $D$ 处用高 1.5 米的测角仪 $A D$ 测得塔顶 $M$ 的仰角为 $30 °$ ，然后沿 $D F$ 方向前行 $70 m$ 到达点 $E$ 处，在点 $E$ 处测得塔顶 $M$ 的仰角为 $60 °$ ．求永定楼的高 $M F$ ．（结果保留根号）

查看试题解析
24. 在美化校园的活动中，某兴趣小组借助如图所示的直角墙角（墙角两边 $D C$ 和 $D A$ 足够长），用 $28 m$ 长的篱笆围成一个矩形花园 $A B C D$ （篱笆只围 $A B$ 和 $B C$ 两边）．设 $A B = x m$ ， $S_{矩形 A B C D} = y m^{2}$ ．

(1)、求 $y$ 与 $x$ 之间的关系式，并写出自变量的取值范围；

(2)、当矩形花园的面积为 $192 m^{2}$ 时，求 $A B$ 的长；

(3)、如果在点 $P$ 处有一棵树（不考虑粗细），它与墙 $D C$ 和 $D A$ 的距离分别是 $15 m$ 和 $6 m$ ，如果要将这棵树围在矩形花园内部（含边界），直接写出矩形花园面积的最大值．

查看试题解析
25. 如图，AB为⊙O的直径，C为BA延长线上一点，CD是⊙O的切线，D为切点，OF⊥AD于点E，交CD于点F．

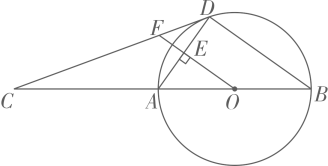(1)、求证：∠ADC=∠AOF；

(2)、若sinC= $\frac{1}{3}$ ，BD=8，求EF的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} - 2 a x + 4 (a > 0)$ ．

(1)、求该抛物线的对称轴和顶点坐标（用含 $a$ 的代数式表示）；

(2)、如果该抛物线的顶点恰好在 $x$ 轴上，求它的表达式；

(3)、如果 $A (m - 1 ， y_{1})$ ， $B (m ， y_{2})$ ， $C (m + 2 ， y_{3})$ 三点均在抛物线 $y = a x^{2} - 2 a x + 4$ 上，且总有 $y_{1} > y_{3} > y_{2}$ ，结合图象，直接写出 $m$ 的取值范围．

查看试题解析
27. 在△ABC中，∠BAC=45°，CD⊥AB于点D ， AE⊥BC于点E ，连接DE ．

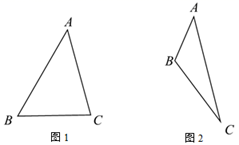(1)、如图1，当△ABC为锐角三角形时，
①依题意补全图形，猜想∠BAE与∠BCD之间的数量关系并证明；

②用等式表示线段AE ， CE ， DE的数量关系，并证明；

(2)、如图2，当∠ABC为钝角时，依题意补全图形并直接写出线段AE ， CE ， DE的数量关系．

查看试题解析
28. 如图，在平面直角坐标系 $x O y$ 中， $C (0 ， 2)$ ， $⊙ C$ 的半径为1．如果将线段 $A B$ 绕原点 $O$ 逆时针旋转 $α (0 ° < α < 180 °)$ 后的对应线段 $A B$ 所在的直线与 $⊙ C$ 相切，且切点在线段 $A B$ 上，那么线段 $A B$ 就是⊙C 的“关联线段”，其中满足题意的最小 $α$ 就是线段 $A B$ 与 $⊙ C$ 的“关联角”．

(1)、如图1，如果 $A (2 ， 0)$ 线段 $O A$ 是 $⊙ C$ 的“关联线段”，那么它的“关联角”为 $°$ ．

(2)、如图2，如果 $A_{1} (- 3 ， 3)$ 、 $B_{1} (- 2 ， 3)$ 、 $A_{2} (1 ， 1)$ 、 $B_{2} (3 ， 2)$ 、 $A_{3} (3 ， 0)$ 、 $B_{3} (3 ， - 2)$ ．那么 $⊙ C$ 的“关联线段”有（填序号，可多选）．
①线段 $A_{1} B_{1}$ ；②线段 $A_{2} B_{2}$ ；③线段 $A_{3} B_{3}$

(3)、如图3，如果 $B (1 ， 0)$ 、 $D (t ， 0)$ ，线段 $B D$ 是 $⊙ C$ 的“关联线段”，那么 $t$ 的取值范围是．

(4)、如图4，如果点 $M$ 的横坐标为 $m$ ，且存在以 $M$ 为端点，长度为 $\sqrt{3}$ 的线段是 $⊙ C$ 的“关联线段”，那么 $m$ 的取值范围是．

查看试题解析