北京市丰台区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-17 类型:期末考试
一、单选题
-
1. 下列是围绕2022年北京冬奥会设计的剪纸图案,其中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,A,B,C是⊙O上的点,如果∠BOC=120°,那么∠BAC的度数是( )
2. 如图,A,B,C是⊙O上的点,如果∠BOC=120°,那么∠BAC的度数是( ) A、90° B、60° C、45° D、30°3. 抛物线的对称轴是( )A、 B、 C、 D、4. 把一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,抽出的牌上的数小于6的概率为( )
A、90° B、60° C、45° D、30°3. 抛物线的对称轴是( )A、 B、 C、 D、4. 把一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,抽出的牌上的数小于6的概率为( ) A、 B、 C、 D、5. 若关于x的一元二次方程有一个解为 , 那么m的值是( )A、-1 B、0 C、1 D、1或-16. 二次函数的图象如图所示,那么下列说法正确的是( )
A、 B、 C、 D、5. 若关于x的一元二次方程有一个解为 , 那么m的值是( )A、-1 B、0 C、1 D、1或-16. 二次函数的图象如图所示,那么下列说法正确的是( )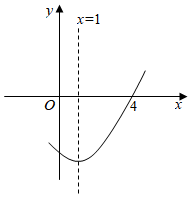 A、 B、 C、 D、7. 如图所示,边长为1的正方形网格中,O,A,B,C,D是网格线交点,若与所在圆的圆心都为点O,那么阴影部分的面积为( )
A、 B、 C、 D、7. 如图所示,边长为1的正方形网格中,O,A,B,C,D是网格线交点,若与所在圆的圆心都为点O,那么阴影部分的面积为( )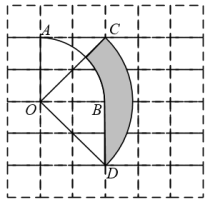 A、 B、 C、 D、8. 如图所示,有一个容器水平放置,往此容器内注水,注满为止.若用h(单位:cm)表示容器底面到水面的高度,用V(单位:)表示注入容器内的水量,则表示V与h的函数关系的图象大致是( )
A、 B、 C、 D、8. 如图所示,有一个容器水平放置,往此容器内注水,注满为止.若用h(单位:cm)表示容器底面到水面的高度,用V(单位:)表示注入容器内的水量,则表示V与h的函数关系的图象大致是( )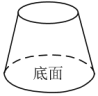 A、
A、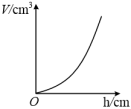 B、
B、 C、
C、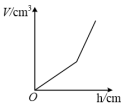 D、
D、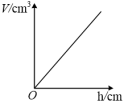
二、填空题
-
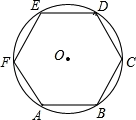
9. 如果点与点B关于原点对称,那么点B的坐标是 .10. 如图,把分成相等的六段弧,依次连接各分点得到正六边形ABCDEF,如果的周长为 , 那么该正六边形的边长是 .
 11. 如图,四边形ABCD内接于 , E为直径AB延长线上一点,且 , 若 , 则的度数为 .
11. 如图,四边形ABCD内接于 , E为直径AB延长线上一点,且 , 若 , 则的度数为 .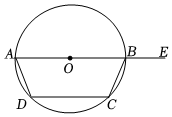 12. 如图所示,绕点P顺时针旋转得到 , 则旋转的角度是 .
12. 如图所示,绕点P顺时针旋转得到 , 则旋转的角度是 .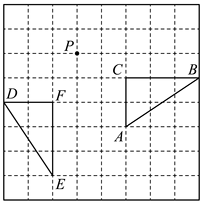 13. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.
13. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.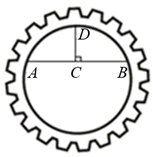 14. 已知抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
14. 已知抛物线上部分点的横坐标x,纵坐标y的对应值如下表:x
…
-2
-1
0
1
2
3
…
y
…
5
0
-3
-4
-3
0
…
那么该抛物线的顶点坐标是 .
15. 小红利用计算机模拟“投针试验”:在一个平面上画一组间距为cm的平行线,将一根长度为cm的针任意投掷在这个平面上,针可能与某一直线相交,也可能与任一直线都不相交.下图显示了小红某次实验的结果,那么可以估计出针与直线相交的概率是(结果保留小数点后两位).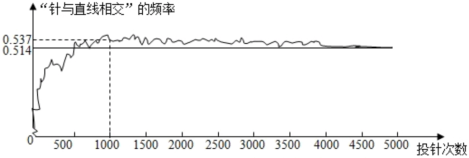 16. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.
16. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.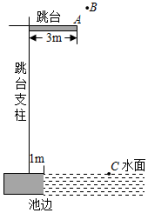
三、解答题
-
17. 计算: .18. 解方程: .19. 下面是小亮设计的“过圆上一点作已知圆的切线”的尺规作图过程.
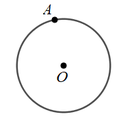
已知:点A在上.
求作:直线PA和相切.
作法:如图,
①连接AO;
②以A为圆心,AO长为半径作弧,与的一个交点为B;
③连接BO;
④以B为圆心,BO长为半径作圆;
⑤作的直径OP;
⑥作直线PA.
所以直线PA就是所求作的的切线.
根据小亮设计的尺规作图过程,
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明:证明:在中,连接BA.
∵ , ,
∴ .
∴点A在上.
∵OP是的直径,
∴( ▲ )(填推理的依据).
∴ .
又∵点A在上,
∴PA是的切线( ▲ )(填推理的依据).
20. 已知关于x的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 , 且该方程的两个实数根的差为1,求k的值.21. 在平面直角坐标系xOy中,抛物线经过点 , .(1)、求抛物线的解析式;(2)、设抛物线与y轴的交点为C,求的面积.22. 小宇和小伟玩“石头、剪刀、布”的游戏.这个游戏的规则是:“剪刀”胜“布”,“布”胜“石头”,“石头”胜“剪刀”,手势相同不分胜负.如果二人同时随机出手(分别出三种手势中的一种手势)一次,那么小宇获胜的概率是多少? 23. 某校举办了“冰雪运动进校园”活动,计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场.如下图所示,已知空地长27m,宽12m,矩形冰场的长与宽的比为4:3,如果要使冰场的面积是原空地面积的 , 并且预留的上、下通道的宽度相等,左、中、右通道的宽度相等,那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米?
23. 某校举办了“冰雪运动进校园”活动,计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场.如下图所示,已知空地长27m,宽12m,矩形冰场的长与宽的比为4:3,如果要使冰场的面积是原空地面积的 , 并且预留的上、下通道的宽度相等,左、中、右通道的宽度相等,那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米?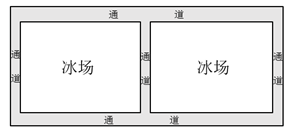 24. 如图,AB是的直径,PA,PC是的切线,A,C是切点,连接AC,PO,交点为D.
24. 如图,AB是的直径,PA,PC是的切线,A,C是切点,连接AC,PO,交点为D.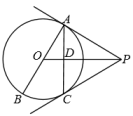 (1)、求证:;(2)、延长PO交于点E,连接BE,CE.若 , , 求AB的长.25. 小朋在学习过程中遇到一个函数 .
(1)、求证:;(2)、延长PO交于点E,连接BE,CE.若 , , 求AB的长.25. 小朋在学习过程中遇到一个函数 .下面是小朋对其探究的过程,请补充完整:
(1)、观察这个函数的解析式可知,x的取值范围是全体实数,并且y有值(填“最大”或“最小”),这个值是;(2)、进一步研究,当时,y与x的几组对应值如下表:x
0
1
2
3
4
…
y
0
2
1
0
2
…
结合上表,画出当时,函数的图象;
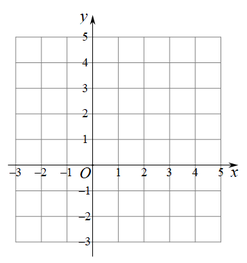 (3)、结合(1)(2)的分析,解决问题:
(3)、结合(1)(2)的分析,解决问题:若关于x的方程有一个实数根为2,则该方程其它的实数根约为(结果保留小数点后一位).
26. 在平面直角坐标系xOy中, , 是抛物线上任意两点.(1)、求抛物线的顶点坐标(用含m的式子表示);(2)、若 , , 比较与的大小,并说明理由;(3)、若对于 , , 都有 , 直接写出m的取值范围.27. 如图,在中, , , D是边BC上一点,作射线AD,满足 , 在射线AD取一点E,且 . 将线段AE绕点A逆时针旋转90°,得到线段AF,连接BE,FE,连接FC并延长交BE于点G. (1)、依题意补全图形;(2)、求的度数;(3)、连接GA,用等式表示线段GA,GB,GC之间的数量关系,并证明.28. 对于平面直角坐标系xOy中的图形M,N,给出如下定义:若图形M和图形N有且只有一个公共点P,则称点P是图形M和图形N的“关联点”.
(1)、依题意补全图形;(2)、求的度数;(3)、连接GA,用等式表示线段GA,GB,GC之间的数量关系,并证明.28. 对于平面直角坐标系xOy中的图形M,N,给出如下定义:若图形M和图形N有且只有一个公共点P,则称点P是图形M和图形N的“关联点”.已知点 , , , .
(1)、直线l经过点A,的半径为2,在点A,C,D中,直线l和的“关联点”是;(2)、G为线段OA中点,Q为线段DG上一点(不与点D,G重合),若和有“关联点”,求半径r的取值范围;(3)、的圆心为点 , 半径为t,直线m过点A且不与x轴重合.若和直线m的“关联点”在直线上,请直接写出b的取值范围.