初中数学北师大版八年级下册第四章第三节公式法同步练习

试卷更新日期：2022-02-17 类型：同步测试

进入出卷网下载

一、单选题

1. 下列多项式能用平方差公式分解因式的是（）

A、4x²+y² B、-4x²-y² C、-4x²+y² D、-4x+y²

查看试题解析
2. 因式分解： $x^{3} - 4 x =$ （）

A、 $x (x^{2} - 4 x)$ B、 $x (x + 4) (x - 4)$ C、 $x (x + 2) (x - 2)$ D、 $x (x^{2} - 4)$

查看试题解析
3. 下列式子直接能用完全平方公式进行因式分解的是（）

A、 $16 a^{2} + 8 a + 1$ B、 $a^{2} - 3 a + 9$ C、 $4 a^{2} + 4 a - 1$ D、 $a^{2} - 8 a - 16$

查看试题解析
4. 若a，b，c分别是 $△$ ABC的三边长，且满足a²﹣2ab+b²＝0，b²﹣c²＝0，则 $△$ ABC的形状是（）

A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
5. a⁴b－6a³b+9a²b分解因式的正确结果是（）

A、a²b（a²－6a+9） B、a²b（a+3）（a－3） C、b（a²－3） D、a²b（a－3） ²

查看试题解析
6. 若一个三角形的三边长为a，b，c，且满足a²-2ab+b²+ac-bc =0，则这个三角形是（）

A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形

查看试题解析
7. 如图，长与宽分别为a、b的长方形，它的周长为14，面积为10，则a³b+2a²b²+ab³的值为（　　）

A、2560 B、490 C、70 D、49

查看试题解析
8. 如图，在长方形 ABCD 中，E 为 AB 中点，以 BE 为边作正方形 BEFG，边 EF 交 CD 于点H，在边 BE 上取点 M 使BM=BC，作 MN∥BG 交 CD 于点 L，交 FG 于点 N．

欧几里得在《几何原本》中利用该图解释了 $(a + b) (a - b) = a^{2} - b^{2}$ ，连结AC，记△ABC的面积为 $S_{1}$ ，图中阴影部分的面积为 $S_{2}$ ．若 $a = 3 b$ ，则 $\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\frac{7}{18}$ C、 $\frac{3}{4}$ D、 $\frac{5}{4}$

查看试题解析

二、填空题

9. 分解因式：7a²﹣63＝

查看试题解析
10. 4x²-(k-1)x+1能用完全平方公式因式分解，则k的值为

查看试题解析
11. 已知x+y＝2，则 $\frac{1}{2}$ （x²+2xy+y²）的值为.

查看试题解析
12. 下列因式分解正确的是（填序号）
① $x^{2} - 2 x = x (x - 2)$ ；② $x^{2} - 2 x + 1 = x (x - 2) + 1$ ；③ $x^{2} - 4 = (x + 4) (x - 4)$ ；④ $4 x^{2} + 4 x + 1 = (2 x + 1)^{2}$

查看试题解析
13. 由多项式与多项式相乘的法则可知：
即：（a＋b）（a²﹣ab＋b²）＝a³﹣a²b＋ab²＋a²b﹣ab²＋b³＝a³＋b³

即：（a＋b）（a²﹣ab＋b²）＝a³＋b³①，我们把等式①叫做多项式乘法的立方和公式．

同理，（a﹣b）（a²＋ab＋b²）＝a³﹣b³②，我们把等式②叫做多项式乘法的立方差公式．

请利用公式分解因式：﹣64x³＋y³＝．

查看试题解析
14. 甲、乙两个同学分解因式x²+ax+b时，甲看错了b ，分解结果为（x+2）（x+4）；乙看错了a ，分解结果为（x+1）（x+9），则多项式x²+ax+b分解因式的正确结果为．

查看试题解析
15. 在实数范围内因式分解：x²﹣3＝， 3x²﹣5x+2＝．

查看试题解析
16. 观察下列各式：
(x−1)(x+1)=x²−1

(x−1)(x²+x+1)=x³−1

(x−1)(x³+x²+x+1)=x $^{4}$ −1…

根据以上规律，求1+2+2²+…+ $2^{2016} + 2^{2017} =$ .

查看试题解析

三、计算题

17. 因式分解

(1)、 $a^{3} b - a b$

(2)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
18. 计算题：

(1)、因式分解：（x²+y²）²-4x²y²；

(2)、计算：8（1+7²）（1+7⁴）（1+7⁸）（1+7¹⁶）.

查看试题解析
19. 利用因式分解进行计算

(1)、 $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \dots \times (1 - \frac{1}{10^{2}})$

(2)、 $(2^{2} + 4^{2} + 6^{2} + 8^{2} + 10^{2}) - (1^{2} + 3^{2} + 5^{2} + 7^{2} + 9^{2})$

查看试题解析

四、解答题

20. 分解因式

(1)、 $9 {(m + n)}^{2} - {(m - n)}^{2}$

(2)、 ${(x^{2} - 6 x)}^{2} + 18 (x^{2} - 6 x) + 81$

(3)、 $- 4 m^{3} + 16 m^{2} - 26 m$

(4)、（a²+4）²﹣16a²

查看试题解析
21. 第一环节：自主阅读材料：
常用的分解因式方法有提公因式、公式法等．但有的多项式只用上述方法就无法分解，如x²-4y²+2x-4y，细心观察这个式子会发现前两项符合平方差公式，后两项可提取公因式，分解过程为：

x²-4y²+2x-4y

=(x²-4y²)+(2x-4y) ……分组

=(x-2y)(x+2y)+2(x-2y) ……组内分解因式

=(x-2y)(x+2y+2) ……整体思想提公因式

这种分解因式的方法叫分组分解法。

第二环节：利用这种方法解决下列问题。

因式分解：x²y-4y-2x²+8．

第三环节：拓展运用。

已知a，b，c为△ABC的三边，且b²+2ab=c²+2ac，试判断△ABC的形状．

查看试题解析
22. 如果n是正整数，求证：3ⁿ⁺²-2ⁿ⁺²+3ⁿ-2ⁿ能被10整除.

查看试题解析

五、综合题

23. 先阅读，再解答下列问题.
已知（a²+b²）-8（a²+b²）²+16=0，求a²+b²的值.

错解：设（a²+b²）²=m，

则原式可化为m²-8m+16=0，

即（m-4）²=0，解得m=4.

由（a²+b²）²=4，得a²+b²=±2

(1)、上述解答过程错在哪里？为什么？

(2)、请你用上述方法分解因式：（a+b）²-14（a+b）+49

查看试题解析
24. 当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式.例如，由图1，可得等式：（a+2b）（a+b）＝a²+3ab+2b².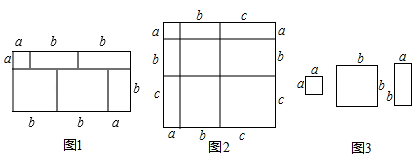

(1)、由图2，可得等式：.

(2)、利用（1）中所得到的结论，解决下面的问题：已知a+b+c＝12，ab+bc+ac＝47，求a²+b²+c²的值；

(3)、利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a²+5ab+2b²＝（2a+b）（a+2b）

查看试题解析
25. （阅读材料）把形如ax²+bx+c的二次三项式（或其一部分）经过适当变形配成完全平方式的方法叫配方法，配方法在因式分解、证明恒等式、利用a²≥0求代数式最值等问题中都有广泛应用.
例如：利用配方法将x²﹣6x+8变形为a（x+m）²+n的形式，并把二次三项式分解因式.

配方：x²﹣6x+8

＝x²﹣6x+3²﹣3²+8

＝（x﹣3）²﹣1

分解因式：x²﹣6x+8

＝（x﹣3）²﹣1

＝（x﹣3+1）（x﹣3﹣1）

＝（x﹣2）（x﹣4）

（解决问题）根据以上材料，解答下列问题：

(1)、利用配方法将多项式x²﹣4x﹣5化成a（x+m）²+n的形式.

(2)、利用配方法把二次三项式x²﹣2x﹣35分解因式.

(3)、若a、b、c分别是 $△$ ABC的三边，且a²+2b²+3c²﹣2ab﹣2b﹣6c+4＝0，试判断 $△$ ABC的形状，并说明理由.

(4)、求证：无论x，y取任何实数，代数式x²+y²+4x﹣6y+15的值恒为正数.

查看试题解析

初中数学北师大版八年级下册第四章第三节 公式法 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

初中数学北师大版八年级下册第四章第三节公式法同步练习