初中数学北师大版八年级下册第二章第六节一元一次不等式组同步练习

试卷更新日期：2022-02-17 类型：同步测试

进入出卷网下载

一、单选题

1. 下列不等式组中，无解的是（）

A、 ${\begin{matrix} x < 2 \\ x < - 3 \end{matrix}$ B、 ${\begin{matrix} x < 2 \\ x > - 3 \end{matrix}$ C、 ${\begin{matrix} x > 2 \\ x > - 3 \end{matrix}$ D、 ${\begin{matrix} x > 2 \\ x < - 3 \end{matrix}$

查看试题解析
2. 已知关于x的不等式组的 ${\begin{cases} x - a \geq b \\ 2 x - a < 2 b + 1 \end{cases}$ 解集为3≤x＜5，则 $\frac{b}{a}$ 的值为（）

A、﹣2 B、 $- \frac{1}{2}$ C、﹣4 D、﹣ $\frac{1}{4}$

查看试题解析
3. 若不等式组 ${\begin{array}{l} x < 1 \\ x < m \end{array}$ 的解为x＜m，则m的取值范围为（）

A、m≤1 B、m=1 C、m≥1 D、m＜1

查看试题解析
4. 定义：对于实数 $a$ ，符号 $[a]$ 表示不大于 $a$ 的最大整数.例如：[3.2]=3，[2]=2，[-2.3]=-3.如果 $[\frac{x - 1}{2}] = 2$ ，则 $x$ 的取值范围是（）

A、 $5 \leq x \leq 7$ B、 $5 < x \leq 7$ C、 $5 < x < 7$ D、 $5 \leq x < 7$

查看试题解析
5. 定义一种运算： $a * b = {\begin{array}{l} a ， a \geq b \\ b ， a < b \end{array}$ ，则不等式 $(2 x + 1) * (2 - x) > 3$ 的解集是（）

A、 $x > 1$ 或 $x < \frac{1}{3}$ B、 $- 1 < x < \frac{1}{3}$ C、 $x > 1$ 或 $x < - 1$ D、 $x > \frac{1}{3}$ 或 $x < - 1$

查看试题解析
6. 已知某程序如图所示，规定：从“输入实数x”到“结果是否大于95”为一次操作，如果该程序进行了两次操作停止，那么实数x的取值范围是 $($ $)$

A、 $x > 23$ B、 $11 \leq x \leq 23$ C、 $23 < x \leq 47$ D、 $x \leq 47$

查看试题解析
7. 若关于x的一元一次不等式组 ${\begin{array}{l} \frac{- 2 x + 3 m}{4} \leq 2 x \\ 2 x + 7 \leq 4 (x + 1) \end{array}$ 的解集为 $x \geq \frac{3}{2}$ ，且关于y的方程 $3 y - 2 = \frac{2 m - (5 - 3 y)}{2}$ 的解为非负整数，则符合条件的所有整数m的积为（）

A、2 B、7 C、11 D、10

查看试题解析
8. 目前，我国已获批上市4款自主研发的新冠疫苗．某生物制药公司计划生产制造A、B两种疫苗共40万支，已知生产每支A疫苗需甲种原料8mg ，乙种原料5mg；生产每支B疫苗需甲种原料4mg ，乙种原料9mg ．公司现有甲种原料4kg ，乙种原料3kg ，设计划生产A疫苗x支，下列符合题意的不等式组是（）

A、 ${\begin{matrix} 8 x + 5 (400000 - x) \leq 4000000 \\ 4 x + 9 (400000 - x) \leq 3000000 \end{matrix}$ B、 ${\begin{matrix} 5 x + 9 (400000 - x) \leq 4000000 \\ 8 x + 4 (400000 - x) \leq 3000000 \end{matrix}$ C、 ${\begin{matrix} 8 x + 4 (400000 - x) \leq 4000000 \\ 5 x + 9 (400000 - x) \leq 3000000 \end{matrix}$ D、 ${\begin{matrix} 8 x + 9 (400000 - x) \leq 4000000 \\ 5 x + 4 (400000 - x) \leq 3000000 \end{matrix}$

查看试题解析

二、填空题

9. 不等式组 ${\begin{array}{l} 5 x + 4 > 3 x \\ \frac{x - 1}{2} \leq \frac{2 x - 1}{5} \end{array}$ 的解是.

查看试题解析
10. 已知关于 $x$ 的不等式组 ${\begin{array}{l} 5 - 3 x \geq - 1 ， \\ a - 2 x < 0 \end{array}$ 无解，则 $a$ 的取值范围是．

查看试题解析
11. 三个数3， 1-a，1-2a在数轴上从左到右依次排列，且以这三个数为边长能构成三角形，则a的取值范围为

查看试题解析
12. 在某种药品的说明书上的部分内容是“用法用量：每天 $30 ~ 60 mg$ ，分2~3次服用”.则一次服用这种药品的剂量 $x$ 的范围是 $mg$ .

查看试题解析
13. 对于任意实数，m，n，定义一种运算： $m ※ n = m n - m - n + \frac{7}{2}$ ，请根据上述定义解决问题：若关于x的不等式 $a < (\frac{1}{2} ※ x) < 7$ 的解集中只有一个整数解，则实数a的取值范围是.

查看试题解析
14. 若点 $P$ 的坐标为 $(\frac{x - 1}{5} ， 2 x - 10)$ ，其中 $x$ 满足不等式组 ${\begin{array}{l} 5 x - 10 \geq 2 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ ，则点 $P$ 在第象限.

查看试题解析
15. 令 a、b 两数中较大的数记作 max|a，b|，如 max|2，3|=3，已知 k 为正整数且使不等式 max|2k+1，﹣k+5|≤5 成立，则 k 的值是.

查看试题解析
16. 12月是成都奶油巧克力草莓大丰收的季节，重庆渝北海领开展“水果一带一路”活动，成都顺丰快递公司出动所有车辆分12月25，26日两批往重庆运输现摘草莓.该公司共有A，B，C三种车型，其中A型车数量占公司车辆总数的一半，B型车数量与C型车数量相等.25日安排A型车数量的一半，B型车数量的 $\frac{1}{3}$ ，C型车数量的 $\frac{3}{4}$ 进行运输，且25日A，B，C三种车型每辆车载货量分别为10吨，15吨，20吨，则25日刚好运完所有草莓重量的一半.26日安排剩下的所有车辆完成剩下的所有草莓的运输，且26日A，B，C三种车型每辆载货量分别不超过14吨，27吨，24吨.26日B型车实际载货量为26日A型车每辆实际载货量的 $\frac{3}{2}$ .已知同型货车每辆的实际载货量相等，A，B，C三种车型每辆车26日运输成本分别为100元/吨，200元/吨，75元/吨，则26日运输时，一辆A型车、一辆B型车，一辆C型车总的运输成本至多为元.

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 6 (\frac{2}{3} x - 2) < x - 3 \\ \frac{1 - x}{2} - 2 ⩽ x \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
18. 已知a，b，c是△ABC的三边长，若b＝2a﹣1，c＝a+5，且△ABC的周长不超过20cm，求a的范围.

查看试题解析
19. $x$ 取哪些正整数值时，不等式 $5 x + 2 > 3 (x - 1)$ 与 $\frac{2 x - 1}{3} \leq \frac{3 x + 1}{6}$ 都成立?

查看试题解析
20. 已知关于x ， y的方程满足方程组 ${\begin{array}{l} 3 x + 2 y = m + 1 ① \\ 2 x + y = m - 1 ② \end{array}$ ，
（Ⅰ）若 x-y=2 ，求m的值；

（Ⅱ）若x ， y ， m均为非负数，求m的取值范围，并化简式子 $| m - 3 | + | m - 5 |$ ；

（Ⅲ）在（Ⅱ）的条件下求 $s = 2 x - 3 y + m$ 的最小值及最大值．

查看试题解析

四、综合题

21. 疫情期间，为满足市民的防护需求，某医药公司想要购买A、B两种口罩．在进行市场调研时发现：A型口罩比B型口罩每件进价多了10元．用68000元购买A型口罩的件数是用32000元购买B型口罩件数的2倍．

(1)、A、B型口罩进价分别为每件多少元？

(2)、若该公司计划购买A、B型口罩共200件，其中A型口罩的件数不大于B型口罩的件数，且用于购买A型口罩的钱数多于购买B型口罩的钱数．设购买A型口罩x件，则符合条件的进货方案共多少种？（件数均为整数，不用列出方案）

查看试题解析
22. 2010年6月5日是第38个世界环境日，世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召，某品牌汽车4S店准备购进A型（电动汽车）和B型（太阳能汽车）两种不同型号的汽车共16辆，以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息：

成本价（万元/辆）

售价（万元/辆）

A型

30

32

B型

42

45

(1)、若经营者的购买资金不少于576万元且不多于600万元，则有哪几种进车方案？

(2)、在（1）的前提下，如果你是经营者，并且所进的汽车能全部售出，你会选择哪种进车方案才能使获得的利润最大？最大利润是多少？

(3)、假设每台电动汽车每公里的用电费用为0.65元，且两种汽车最大行驶里程均为30万公里，那么从节约资金的角度，你做为一名购车者，将会选购哪一种型号的汽车？并说明理由.

查看试题解析
23. 对实数x、y，我们定义一种新运算：F（x，y） $= a x + b y$ （其中a，b为常数）.例如：F（2，3） $= 2 a + 3 b$ ，F（2， $- 3$ ） $= 2 a - 3 b$ .已知F（1，1）=2，F（1， $- 1$ ）=0.

(1)、则 $a =$ ， $b =$ ；

(2)、若方程组 ${\begin{array}{l} F (x ， - y) = 4 m - 3 \\ F (x ， 2 y) = - 5 m \end{array}$ 的解中，x是非正数，y是负数：
①求m的取值范围；

②若 $2^{x} \cdot 4^{y} = 2^{n}$ ，求n的最小值；

(3)、若关于x的不等式组 ${\begin{array}{l} F (3 x ， 0) > - 2 c \\ F (- 2 x ， 0) \geq - 3 c \end{array}$ 恰好有3个整数解，求c的取值范围.

查看试题解析
24. 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元．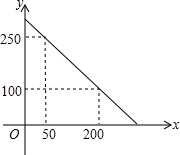

(1)、根据图象，求y与x之间的函数关系式；

(2)、求甲、乙两种品牌的文具盒进货单价；

(3)、若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？

查看试题解析

	成本价（万元/辆）	售价（万元/辆）
A型	30	32
B型	42	45

初中数学北师大版八年级下册第二章第六节 一元一次不等式组 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

初中数学北师大版八年级下册第二章第六节一元一次不等式组同步练习