初中数学北师大版八年级下册第二章第四节一元一次不等式同步练习

试卷更新日期：2022-02-17 类型：同步测试

进入出卷网下载

一、单选题

1. 在式子－3＜0，x≥2，x＝a，x²－2x，x≠3，x＋1＞y中，是不等式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 不等式 $2 x + 3 \geq 1$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
3. 实数a在数轴上的对应点的位置如图所示．若实数b满足－a+1＜b＜a，则b的值可以是（）

A、－1 B、1 C、－2 D、2

查看试题解析
4. 一款皮大衣进价2000元，标价3000元，若商场要求以利润率不低于5%的售价打折出售，则售货员出售此商品最低可打（）

A、六折 B、七折 C、八折 D、九折

查看试题解析
5. 若关于x的不等式mx﹣n＞0的解集是x＜ $\frac{1}{5}$ ，则关于x的不等式（m+n）x＞n﹣m的解集是（　　）

A、x＜﹣ $\frac{2}{3}$ B、x＞﹣ $\frac{2}{3}$ C、x＜ $\frac{2}{3}$ D、x＞ $\frac{2}{3}$

查看试题解析
6. 不等式2x﹣6≤0的非负整数解的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 关于x的不等式x-b>0恰有两个负整数解，则b的取值范围是（）

A、-3<b<-2 B、-3<b≤-2 C、-3≤b≤-2 D、-3≤b<-2

查看试题解析
8. 随看科技的进步，我们可以通过手机APP实时查看公交车到站情况．小明想乘公交车，可又不想静静地等在A站．他从A站往B站走了一段路，拿出手机查看了公交车到站情况，发现他与公交车的距离为720m（如图），此时有两种选择：

（ 1 ）与公交车相向而行，到A公交站去乘车；（2）与公交车同向而行，到B公交站去乘车．假设小明的速度是公交车速度的 $\frac{1}{5}$ ，若要保证小明不会错过这辆公交车，则A，B两公交站之间的距离最大为（）

A、240m B、300m C、320m D、360m

查看试题解析

二、填空题

9. 若（m﹣1）x^|m|+3＞0是关于x的一元一次不等式，则m＝．

查看试题解析
10. 不等式 $2 x - 1 > \frac{1}{2} x$ 的解集是.

查看试题解析
11. 某种药品的说明书上贴有如图所示的标签，一次服用药品的剂量设为 $x$ ，则 $x$ 的取值范围是．

查看试题解析
12. 关于x的不等式 $(2 a - b) x + a - 5 b > 0$ 的解集是 $x < 1$ ，则关于x的不等式 $2 a x - b > 0$ 的解集是．

查看试题解析
13. 若代数式 $\frac{t + 1}{5}$ ﹣ $\frac{t - 1}{2}$ 的值不小于﹣3，则t的取值范围是．

查看试题解析
14. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - y = a + 3 \\ 2 x + y = 5 a \end{array}$ 的解 $x$ ， $y$ 都为正数，满足不等式 $| a | + | 4 - a | < 6$ 成立的整数 $a$ 的值为（写一个即可）.

查看试题解析
15. 一次知识竞赛一共有22道题目，答对一题得5分，不答得0分，答错一题扣2分，小明有二题没有答，成绩超过75分，则小明至多答错了道题

查看试题解析
16. 若一个奇数的立方根比3大，平方根比6小，且能被5整除，则这个数一定是

查看试题解析

三、解答题

17. 解一元一次不等式 $\frac{1 - x}{2} - 6 < \frac{x - 4}{3}$ ，并把它的解集在数轴上表示出来.

查看试题解析
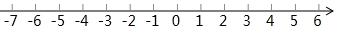18. 某店主购进 $A$ ， $B$ 两种礼盒.已知 $A$ ， $B$ 两种礼盒的单价比为2∶3，单价和为10元.该店主进 $B$ 种礼盒的数量是 $A$ 种礼盒数量的2倍少1个，且这两种礼盒花费不超过398元，则 $A$ 种礼盒最多购买多少个？

查看试题解析
19. 已知方程 $\frac{x - (2 x - a)}{2} = 2$ 的解为负数，求正整数 $a$ 的值.

查看试题解析

四、综合题

20. 2020年上半年，我市出境旅游旅客的消费额比2019年同期相比至少下降了60%的消费．

(1)、若2020年我市上半年出境旅游旅客消费额共计20亿元，则2019年我市出境旅游旅客消费额至少多少亿元？

(2)、在疫情期间，我市 $A$ ， $B$ 两旅游公司的出境旅游业务也受到严重的影响．现知，我市 $A$ 旅游公司2019年出境旅游旅客消费额比2018年增长 $\frac{4}{3} a %$ ，但2020年比2019年出境旅游旅客消费额减少了 $3 a %$ ； $B$ 旅游公司2020年出境旅游旅客消费额比 $A$ 旅游公司2019年出境旅游旅客消费额少 $a %$ ．已知2020年 $A$ 、 $B$ 旅游公司出境旅游旅客消费总额是2018年 $A$ 旅游公司出境旅游旅客消费额的 $\frac{16}{3} a %$ ，求 $a$ 的值．

查看试题解析
21.

(1)、 $2 x - 11 < 4 (x - 3) + 3$ ，并把它的解集在数轴上表示出来.

(2)、已知关于x的不等式（m﹣1）x＞6，两边同除以m﹣1，得x＜ $\frac{6}{m - 1}$ ，试化简：|m﹣1|﹣|2﹣m|.

查看试题解析
22. 某商场同时购进甲、乙、丙三种商品共100件，总进价为6 800元，其每件的进价和售价如下表：

商品名称

甲

乙

丙

进价（元/件）

40

70

90

售价（元/件）

60

100

130

设甲种商品购进x件，乙种商品购进y件．

(1)、商场要求购进的乙种商品数量不超过甲种商品数量，求甲种商品至少购进多少件？

(2)、若销售完这些商品获得的最大利润是3 100元，求甲种商品最多购进多少件？

查看试题解析
23. 阅读下面材料：
小明在数学课外小组活动时遇到这样一个问题：

如果一个不等式中含有绝对值，并且绝对值符号中含有未知数，我们把这个不等式叫做绝对值不等式，求绝对值不等式 $| x | > 3$ 的解集．

小明同学的思路如下：

先根据绝对值的定义，求出 $| x |$ 恰好是 $3$ 时 $x$ 的值，并在数轴上表示为点 $A ， B$ ，如图所示．观察数轴发现，以点 $A ， B$ 为分界点把数轴分为三部分：

点 $A$ 左边的点表示的数的绝对值大于 $3$ ；

点 $A ， B$ 之间的点表示的数的绝对值小于 $3$ ；

点 $B$ 右边的点表示的数的绝对值大于 $3$ ．

因此，小明得出结论绝对值不等式 $| x | > 3$ 的解集为： $x < - 3$ 或 $x > 3$ ．

参照小明的思路，解决下列问题：

(1)、请你直接写出下列绝对值不等式的解集．
① $| x | > 2$ 的解集是．

② $| x | < 5$ 的解集是．

(2)、求绝对值不等式 $2 | x - 2.5 | + 4 < 6$ 的解集．

(3)、如果（2）中的绝对值不等式的整数解，都是关于 $x$ 的不等式组 ${\begin{matrix} x < 2 x - m \\ x - 2 \leq m \end{matrix}$ 的解，求 $m$ 的取值范围．

(4)、直接写出不等式 $x^{2} > 16$ 的解集是．

查看试题解析
24. 某杨梅经销商以每千克40元的价格分三批向果农购进杨梅，均分拣成“特优”和“普通”两类销售，分拣和包装费用为每千克6元．每批杨梅中最差的10%不能销售，为损耗，其余杨梅均能售完．“特优”杨梅售价是每千克110元，“普通”杨梅售价为每千克30元．

(1)、该经销商购进的第一批杨梅为500千克，分拣出“特优”杨梅150千克，则他获得的利润是元；

(2)、该经销商购进的第二批杨梅为800千克，获利4800元，求其中售出“特优”和“普通”杨梅各多少千克？

(3)、该经销商希望自己第三批杨梅的销售的利润率不少于35%，他收购杨梅时要确保能分拣出“特优”杨梅占收购总量的百分比至少要达到多少（精确到1%）？（利润＝销售收入﹣总成本，利润率＝ $\frac{利润}{总成本}$ ×100%）

查看试题解析

商品名称	甲	乙	丙
进价（元/件）	40	70	90
售价（元/件）	60	100	130

初中数学北师大版八年级下册第二章第四节 一元一次不等式 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

初中数学北师大版八年级下册第二章第四节一元一次不等式同步练习