初中数学北师大版八年级下册第一章第三节 线段的垂直平分线 同步练习
试卷更新日期:2022-02-16 类型:同步测试
一、单选题
-
1. 如图,在 中, 的垂直平分线交 于点D,交 于点E,连接 .若 , 的周长为13,则 的周长为( )
 A、19 B、16 C、29 D、182. 下列选项中的尺规作图,能推出PA=PC的是( )A、
A、19 B、16 C、29 D、182. 下列选项中的尺规作图,能推出PA=PC的是( )A、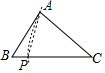 B、
B、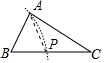 C、
C、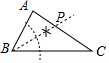 D、
D、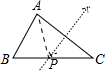 3. “已知等腰三角形的底边和底边上的高,用尺规作图求作等腰三角形”里用到的基本作图是A、作一条线段等于已知线段,作已知线段的垂直平分线 B、作已知角的平分线 C、过直线外一点作已知直线的垂线 D、作一个角等于已知角4. 如图,在△ABC中, AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE的度数为( )
3. “已知等腰三角形的底边和底边上的高,用尺规作图求作等腰三角形”里用到的基本作图是A、作一条线段等于已知线段,作已知线段的垂直平分线 B、作已知角的平分线 C、过直线外一点作已知直线的垂线 D、作一个角等于已知角4. 如图,在△ABC中, AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE的度数为( ) A、68° B、62° C、66° D、56°5. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A、68° B、62° C、66° D、56°5. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( ) A、5 B、4 C、3 D、26. 如图是李老师在黑板上演示的尺规作图及其步骤,
A、5 B、4 C、3 D、26. 如图是李老师在黑板上演示的尺规作图及其步骤,已知钝角 ,尺规作图及步骤如下:
步骤一:以点 为圆心, 为半径画弧;
步骤二:以点 为圆心, 为半径画弧,两弧交于点 ;
步骤三:连接 ,交 延长线于点 .

下面是四位同学对其做出的判断:
小明说: ;
小华说: ;
小强说: ;
小方说: .
则下列说法正确的是( )
A、只有小明说得对 B、小华和小强说的都对 C、小强和小方说的都不对 D、小明和小方说的都对7. 如图,在△ABC中,AB=AC,∠BAC=46°,∠BAC的平分线与AB的垂直平分线OD交于点O,点E在BC上,点F在AC上,连接EF.将∠C沿EF折叠,点C与点O恰好重合时,则∠OEC的度数( ) A、90° B、92° C、95° D、98°8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP,并廷长交BC于点D,则下列说法中正确的个数是( )
A、90° B、92° C、95° D、98°8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP,并廷长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④若AD=2dm,则点D到AB的距离是1dm
⑤S△DAC:S△DAB=1:2
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. 如图,△ABC中,AC=6,BC=4,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为.
 10. 如图,在 中, , , 垂直平分 ,垂足为Q,交 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边 于点D,E;②分别以点D,E为圆心,以大于 的长为半径作弧,两弧相交于点F;⑤作射线 .若 与 的夹角为 ,则 °.
10. 如图,在 中, , , 垂直平分 ,垂足为Q,交 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边 于点D,E;②分别以点D,E为圆心,以大于 的长为半径作弧,两弧相交于点F;⑤作射线 .若 与 的夹角为 ,则 °. 11. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 .
11. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 . 12. 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.∠BAC=75°,则∠B的度数为.
12. 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.∠BAC=75°,则∠B的度数为. 13. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
13. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .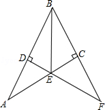 14. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
14. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .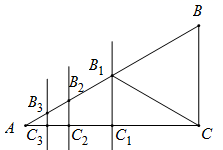 15. 如图,已知△ABC中,OE、OF分别是AB、AC的垂直平分线,∠OBC,∠OCB的平分线相交于点I,有如下结论:①AO=CI;②∠ABC+∠ACO=90°;③∠BOI=∠COI;④OI⊥BC.其中正确的结论是 .
15. 如图,已知△ABC中,OE、OF分别是AB、AC的垂直平分线,∠OBC,∠OCB的平分线相交于点I,有如下结论:①AO=CI;②∠ABC+∠ACO=90°;③∠BOI=∠COI;④OI⊥BC.其中正确的结论是 .
三、作图题
-
16. 作图题:如图,已知 ABC,在BC上找一点D,使 ABD的周长等于AB+BC.(尺规作图,不写作法,保留作图痕迹)

四、解答题
-
17. 如图,在△ABC中,ME和NF分别垂直平分AB和AC.

(1) 若BC = 10 cm,试求△AMN的周长.
(2) 在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
18. 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点D,△ABC和△DBC的周长分别是60cm和38cm,求AB,BC. 19. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
19. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.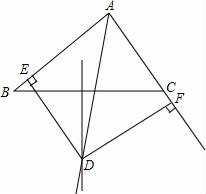
五、综合题
-
20. 如图1所示,在 中, , 的垂直平分线交 于点 ,交 或 的延长线于点 .
 (1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.21. 如图,在 中, 边的垂直平分线 交 于点 , 边的垂直平分线 交 于点 , 与 相交于点 ,连结 , , ,若 的周长为 , 的周长为 .
(1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.21. 如图,在 中, 边的垂直平分线 交 于点 , 边的垂直平分线 交 于点 , 与 相交于点 ,连结 , , ,若 的周长为 , 的周长为 . (1)、求线段 的长;(2)、求线段 的长.22. 如图
(1)、求线段 的长;(2)、求线段 的长.22. 如图
(了解概念)如图1,已知 , 为直线 同侧的两点,点 为直线 的一点,连接 , ,若 ,则称点 为点 , 关于直线 的“等角点”.
(1)、(理解运用)如图2,在 中, 为 上一点,且与点 关于直线 对称,连接 并延长至点 ,判断点 是否为点 , 关于直线 的“等角点”,并说明理由;
(2)、(拓展提升)如图2,在(1)的条件下,若 , ,点 是射线 上一点,且点 , 关于直线 的“等角点”为点 ,请利用尺规在图2中确定点 的位置,并求出 的度数;
(3)、如图3,在 中, , 的平分线交于点 ,点 到 的距离为 ,直线 垂直平分边 ,点 为点 , 关于直线 的“等角点”,连接 , ,当 时, 的值为.23. 如图,直线AB:y=x-4与x轴交于点A,与y轴交于点B,若点E在线段AB上,OE⊥OF,且OE=OF,连接AF. (1)、直接写出点A,B的坐标,并求出线段AB的长.(2)、猜想线段AF与BE之间的数量与位置关系,并证明;(3)、过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE= ,求CF的长.
(1)、直接写出点A,B的坐标,并求出线段AB的长.(2)、猜想线段AF与BE之间的数量与位置关系,并证明;(3)、过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE= ,求CF的长.
-