初中数学北师大版八年级下册第一章第二节 直角三角形 同步练习
试卷更新日期:2022-02-16 类型:同步测试
一、单选题
-
1. 如图, , ,垂足分别是E,F,且 ,若利用“ ”证明 ,则需添加的条件是( )
 A、 B、 C、 D、2. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、83. 如图,一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A、 B、 C、 D、2. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、83. 如图,一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( ) A、6米 B、8米 C、10米 D、12米4. 下列各组数不能组成直角三角形的是( )A、6、8、10 B、 、 、 C、3k、4k、5k(k为正整数) D、8、15、175. 如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光?( )
A、6米 B、8米 C、10米 D、12米4. 下列各组数不能组成直角三角形的是( )A、6、8、10 B、 、 、 C、3k、4k、5k(k为正整数) D、8、15、175. 如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光?( ) A、4米 B、3米 C、5米 D、7米6. 如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A、4米 B、3米 C、5米 D、7米6. 如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( ) A、12cm2 B、18cm2 C、22cm2 D、36cm27. 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,连结AD,AE是∠BAD的平分线,DF∥AB交AE的延长线于点F,若EF=3,则AE的长是( )
A、12cm2 B、18cm2 C、22cm2 D、36cm27. 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,连结AD,AE是∠BAD的平分线,DF∥AB交AE的延长线于点F,若EF=3,则AE的长是( )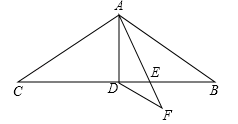 A、3 B、6 C、9 D、128. 如图,在 中, 是 延长线上一点, 是边 上一动点, 连结 ,作 与 关于 对称 (点 与点 对应),连结 ,则 长的最小值是( )
A、3 B、6 C、9 D、128. 如图,在 中, 是 延长线上一点, 是边 上一动点, 连结 ,作 与 关于 对称 (点 与点 对应),连结 ,则 长的最小值是( )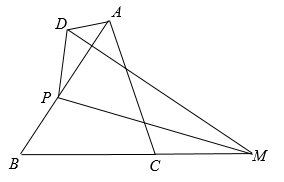 A、0.5 B、0.6 C、 D、9. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( )
A、0.5 B、0.6 C、 D、9. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③
A、①②④ B、①②③④ C、②③④ D、①③二、填空题
-
10. 如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“”.
 11. 如右图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12 cm,则CD =cm.
11. 如右图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12 cm,则CD =cm. 12. 已知直角三角形一个锐角60°,斜边长为4,那么此直角三角形斜边上的的高是.13. 如图,△ABC的三个顶点均在小方格的格点上,BD⊥AC于点D.若每个小方格的边长为1,则BD的长为 .
12. 已知直角三角形一个锐角60°,斜边长为4,那么此直角三角形斜边上的的高是.13. 如图,△ABC的三个顶点均在小方格的格点上,BD⊥AC于点D.若每个小方格的边长为1,则BD的长为 .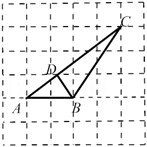 14. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为.
14. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为. 15. 如图,等腰△ABC中,AB=AC=5,BC=6,BD⊥AC,则BD=.
15. 如图,等腰△ABC中,AB=AC=5,BC=6,BD⊥AC,则BD=. 16. 如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=度.
16. 如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=度. 17. 将一副三角尺如图所示叠放在一起,若AB=4cm,则阴影部分的面积是cm2 .
17. 将一副三角尺如图所示叠放在一起,若AB=4cm,则阴影部分的面积是cm2 . 18. 如图,在△ABC中,AB=AC,∠BAC=90°,点D、点E在直线BC上,点F为AE上一点,连接BF,分别交AD、AC于点G、点H,若∠BAD=∠CAE,∠AGH=∠E,AF+AD=BF,AC=3 , 则AE的长为 .
18. 如图,在△ABC中,AB=AC,∠BAC=90°,点D、点E在直线BC上,点F为AE上一点,连接BF,分别交AD、AC于点G、点H,若∠BAD=∠CAE,∠AGH=∠E,AF+AD=BF,AC=3 , 则AE的长为 .
三、解答题
-
19. 如图所示,在 中, ,AD平分 交BC于D, 于E,求证 的周长等于AB的长
 20. 如图,在 中, 于点D , 若 ,求 的长.
20. 如图,在 中, 于点D , 若 ,求 的长. 21. 如图,已知:在△ABC中,AB=AC,∠BAC=120°,D为BC边的中点,DE⊥AC.求证:CE=3AE.
21. 如图,已知:在△ABC中,AB=AC,∠BAC=120°,D为BC边的中点,DE⊥AC.求证:CE=3AE. 22. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程.
22. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程. 23. 如图,把一副三角板如图甲放置,其中 , , ,斜边 , ,把三角板 绕点C顺时针旋转15°得到 (如图乙).这时 与 相交于点O, 与 相交于点F.求线段 的长.
23. 如图,把一副三角板如图甲放置,其中 , , ,斜边 , ,把三角板 绕点C顺时针旋转15°得到 (如图乙).这时 与 相交于点O, 与 相交于点F.求线段 的长. 24. 如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求AC和DC的长.
24. 如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求AC和DC的长. 25. 如图,在等边 中,点 (2,0),点 是原点,点 是 轴正半轴上的动点,以 为边向左侧作等边 ,当 时,求 的长.
25. 如图,在等边 中,点 (2,0),点 是原点,点 是 轴正半轴上的动点,以 为边向左侧作等边 ,当 时,求 的长.
四、综合题
-
26. 如图,在 中, 是角平分线, 于点 , 在边AC上, .
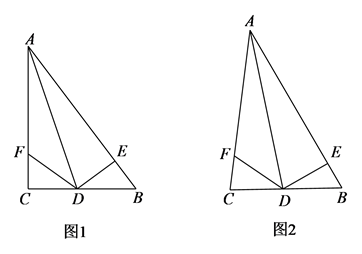 (1)、如图1,若 ,求证: ;(2)、如图2,求证: ;(3)、若 , , ,直接写出 的长.27. 如图,在Rt中, , , , 动点D从点C出发,沿边向点B运动,到点B时停止,若设点D运动的时间为秒.点D运动的速度为每秒1个单位长度.
(1)、如图1,若 ,求证: ;(2)、如图2,求证: ;(3)、若 , , ,直接写出 的长.27. 如图,在Rt中, , , , 动点D从点C出发,沿边向点B运动,到点B时停止,若设点D运动的时间为秒.点D运动的速度为每秒1个单位长度. (1)、当时, , ;(2)、用含t的代数式表示的长;(3)、当点D在边CA上运动时,求t为何值,是以BD或CD为底的等腰三角形?并说明理由;(4)、直接写出当是直角三角形时,t的取值范围 .28. 已知:在△ABC中,∠ABC=90°,点D为直线BC上一点,连接AD并延长,过点C作AC的垂线交AD的延长线于点E.
(1)、当时, , ;(2)、用含t的代数式表示的长;(3)、当点D在边CA上运动时,求t为何值,是以BD或CD为底的等腰三角形?并说明理由;(4)、直接写出当是直角三角形时,t的取值范围 .28. 已知:在△ABC中,∠ABC=90°,点D为直线BC上一点,连接AD并延长,过点C作AC的垂线交AD的延长线于点E. (1)、如图1,若∠BAC=60°,CE= AC,AB=1,求线段AE的长度;(2)、如图2,若AC=EC,点F是线段BA延长线上一点,连接EF与BC交于点H,且∠BAD=∠ACF,求证:AF=2BH;(3)、如图3,AB=2,BC=6,点M为AE中点,连接BM,CM,当|CM-BM|最大时,直接写出△BMC的面积.
(1)、如图1,若∠BAC=60°,CE= AC,AB=1,求线段AE的长度;(2)、如图2,若AC=EC,点F是线段BA延长线上一点,连接EF与BC交于点H,且∠BAD=∠ACF,求证:AF=2BH;(3)、如图3,AB=2,BC=6,点M为AE中点,连接BM,CM,当|CM-BM|最大时,直接写出△BMC的面积.