初中数学北师大版八年级下册第一章第一节第4课时 等边三角形的判定及含30°角的直角三角形的性质 同步练习
试卷更新日期:2022-02-16 类型:同步测试
一、单选题
-
1. 如图,正方形ABCD外侧作等边三角形ADE,则∠AEB的度数为( )
 A、30° B、20° C、15° D、10°2. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴3. 如图,在 中, , 是 边上的高, ,则下列结论中正确的是( )
A、30° B、20° C、15° D、10°2. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴3. 如图,在 中, , 是 边上的高, ,则下列结论中正确的是( ) A、 B、 C、 D、4. 图1是一个地铁站入口的双翼闸机.如图2,当双翼收起时,可以通过闸机的物体的最大宽度是64cm,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA=∠BDQ=30°,则双翼的边缘AC、BD(AC=BD)的长度为( )
A、 B、 C、 D、4. 图1是一个地铁站入口的双翼闸机.如图2,当双翼收起时,可以通过闸机的物体的最大宽度是64cm,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA=∠BDQ=30°,则双翼的边缘AC、BD(AC=BD)的长度为( ) A、 cm B、 cm C、27cm D、54cm5. 如图,是等边中边上的点, , , 则是( )
A、 cm B、 cm C、27cm D、54cm5. 如图,是等边中边上的点, , , 则是( )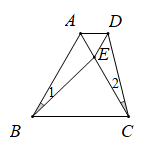 A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定6. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )
A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定6. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )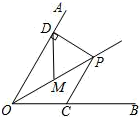 A、 B、 C、 D、7. 如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
A、 B、 C、 D、7. 如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( ) A、1 B、 C、 D、28. 如图,在 中, , ,D为 的中点,P为 上一点,E为 延长线上一点,且 有下列结论:① ;② 为等边三角形;③ ;④ 其中正确的结论是( )
A、1 B、 C、 D、28. 如图,在 中, , ,D为 的中点,P为 上一点,E为 延长线上一点,且 有下列结论:① ;② 为等边三角形;③ ;④ 其中正确的结论是( ) A、①②③④ B、①② C、①②④ D、③④
A、①②③④ B、①② C、①②④ D、③④二、填空题
-
9. 中,∠C=90°,∠A=30°,若BC=3,则AB=.10. 在△ABC中,AC=3,AB= ,∠BAC=150°,S△ABC=.11. 如图,在等边△ABC中,E为AC边的中点,AD垂直平分BC,P是AD上的动点.若AD=6,则EP+CP的最小值为.
 12. 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=
12. 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM= 13. 如图,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,则折痕BE的长为 .
13. 如图,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,则折痕BE的长为 . 14. 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么△PQR的周长等于
14. 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么△PQR的周长等于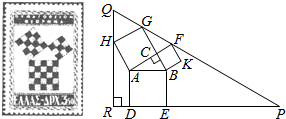 15. 如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是.
15. 如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是.
三、解答题
-
16. 如图,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
 17. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.
17. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.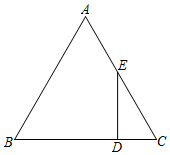 18. 如图所示,A,B两地之间有一座山,汽车原来从A地到B地时需经过C地沿折线A→C→B行驶,开通隧道后,汽车直接沿直线AB行驶.已知AC=10 km,∠A=30°∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?
18. 如图所示,A,B两地之间有一座山,汽车原来从A地到B地时需经过C地沿折线A→C→B行驶,开通隧道后,汽车直接沿直线AB行驶.已知AC=10 km,∠A=30°∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米? 19. 已知点P是线段MN上一动点,分别以PM,PN为一边,在MN的同侧作△APM,△BPN,并连接BM,AN.
19. 已知点P是线段MN上一动点,分别以PM,PN为一边,在MN的同侧作△APM,△BPN,并连接BM,AN.
(Ⅰ)如图1,当PM=AP,PN=BP且∠APM=∠BPN=90°时,试猜想BM,AN之间的数量关系与位置关系,并证明你的猜想;
(Ⅱ)如图2,当△APM,△BPN都是等边三角形时,(Ⅰ)中BM,AN之间的数量关系是否仍然成立?若成立,请证明你的结论;若不成立,试说明理由.
(Ⅲ)在(Ⅱ)的条件下,连接AB得到图3,当PN=2PM时,求∠PAB度数.
20. 点P为等边的边AB延长线上的动点,点B关于直线PC的对称点为D,连接AD. (1)、如图1,若 , 依题意补全图形,并直接写出线段AD的长度;(2)、如图2,线段AD交PC于点E,
(1)、如图1,若 , 依题意补全图形,并直接写出线段AD的长度;(2)、如图2,线段AD交PC于点E,①设 , 求的度数;
②求证: .
四、综合题
-
21. 如图
 (1)、如图1,已知:在ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.(提示:由于DE=AD+AE,证明AD=CE,AE=BD即可)(2)、如图2,将(1)中的条件改为:在ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且ABF和ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明DEF是等边三角形.22. 如图1,在边长为的等边∆中,点是边上一个动点,过点作⊥于点.
(1)、如图1,已知:在ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.(提示:由于DE=AD+AE,证明AD=CE,AE=BD即可)(2)、如图2,将(1)中的条件改为:在ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且ABF和ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明DEF是等边三角形.22. 如图1,在边长为的等边∆中,点是边上一个动点,过点作⊥于点. (1)、求证:;(2)、如图2,过点向引垂线交于点 , 当时,试判断点在上的位置,并说明理由;(3)、如图3,延长至 , 使 , 连接交于点 , 随着点的移动,请判断线段的长度是否发生变化;若变化,请说明理由;若不变,请求出的值.
(1)、求证:;(2)、如图2,过点向引垂线交于点 , 当时,试判断点在上的位置,并说明理由;(3)、如图3,延长至 , 使 , 连接交于点 , 随着点的移动,请判断线段的长度是否发生变化;若变化,请说明理由;若不变,请求出的值.