2021-2022苏科版数学七年级下册9.2单项式乘多项式同步练习（培优）

试卷更新日期：2022-02-15 类型：同步测试

进入出卷网下载

一、单选题

1. 某同学在计算 $- 3 x^{2}$ 乘一个多项式时错误的计算成了加法，得到的答案是 $x^{2} - x + 1$ ，由此可以推断正确的计算结果是（）

A、 $4 x^{2} - x + 1$ B、 $x^{2} - x + 1$ C、 $- 12 x^{4} + 3 x^{3} - 3 x^{2}$ D、无法确定

查看试题解析
2. 下列计算正确的是（）

A、 $2 m + 3 n = 5 m n$ B、 $x^{2} + 2 x^{2} = 3 x^{4}$ C、 $- a^{2} b + b a^{2} = 0$ D、 $3 (a + b) = 3 a + b$

查看试题解析
3. 计算 ${(- x y)}^{3} \cdot (7 x y^{2} - 9 x^{2} y)$ 正确的是（）

A、 $- 7 x^{2} y^{5} + 9 x^{3} y^{4}$ B、 $7 x^{2} y^{5} - 9 x^{3} y^{4}$ C、 $- 7 x^{4} y^{5} + 9 x^{5} y^{4}$ D、 $7 x^{4} y^{5} + 9 x^{5} y^{4}$

查看试题解析
4. 下列运算中不正确的是（　　）

A、3xy﹣（x²﹣2xy）=5xy﹣x² B、5x（2x²﹣y）=10x³﹣5xy C、5mn（2m+3n﹣1）=10m²n+15mn²﹣1 D、（ab）²（2ab²﹣c）=2a³b⁴﹣a²b²c

查看试题解析
5. 要使（﹣6x³）（x²+ax+5）+3x⁴的结果中不含x⁴项，则a的值是（　　）

A、0 B、 $\frac{1}{2}$ C、- $\frac{1}{2}$ D、2

查看试题解析
6. 今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记复习，发现一道题： $- 3 xy (4 y - 2 x - 1) = - 12 {xy}^{2} + 6 x^{2} y + □$ ， $□$ 的地方被钢笔水弄污了，你认为 $□$ 内上应填写 $($ $)$

A、3xy B、 $- 3 xy$ C、 $- 1$ D、1

查看试题解析
7. 要使（x²+ax+1）（﹣6x³）的展开式中不含x⁴项，则a应等于（）

A、6 B、﹣1 C、 $\frac{1}{6}$ D、0

查看试题解析

二、填空题

8. 计算：
（1）（﹣12a²b²c）•（ $- \frac{1}{4}$ abc²）²= ；
（2）（3a²b﹣4ab²﹣5ab﹣1）•（﹣2ab²）= 。

查看试题解析
9. 计算：﹣2a²（a﹣3ab）= ．

查看试题解析
10.
规定一种运算：，其中a、b为实数，则等于．

查看试题解析
11. 不论x为何值，等式x（2x+a）+4x﹣3b=2x²+5x+b恒成立，则a，b的值应分别是．

查看试题解析
12. 已知a+2b=0，则式子a³+2ab（a+b）+4b³的值是．

查看试题解析
13. 用“⊗”定义新运算：对于任意实数a、b，都有a⊗b=b²+1，例如：7⊗4=4²+1=17，那么2015⊗3=；当m为实数时，m⊗（m⊗2）= ．

查看试题解析
14. A、B为单项式，且5x（A﹣2y）=30x²y³+B，则A= ， B= ．

查看试题解析

三、解答题

15. 如果 ${(- 3 x)}^{2} (x^{2} - 2 n x + \frac{2}{3})$ 的展开式中不含x³项，求n的值．

查看试题解析
16. 已知有理数a、b、c满足|a﹣b﹣3|+（b+1）²+|c﹣1|=0，求（﹣3ab）•（a²c﹣6b²c）的值．

查看试题解析
17. 请先阅读下列解题过程，再仿做下面的题．
已知x²+x-1=0，求x³+2x²+3的值．
解：x³+2x²+3=x³+x²-x+x²+x+3
=x（x²+x-1）+x²+x-1+4
=0+0+ 4=4
如果1+x +x²+x³=0，求x+x²+x³+x⁴+x⁵+ x⁶+x⁷+x⁸的值．

查看试题解析
18. 先阅读再解答：我们已经知道，根据几何图形的面积关系可以说明完全平方公式，实际上还有一些等式也可以用这种方式加以说明，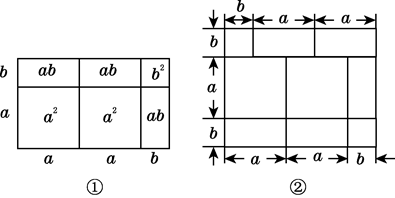

例如：

(2a＋b)(a＋b)＝2a²＋3ab＋b² ，就可以用图①的面积关系来说明．

(1)、根据图②写出一个等式：；

(2)、已知等式：(x＋p)(x＋q)＝x²＋(p＋q)x＋pq，请你画出一个相应的几何图形加以说明．

查看试题解析