初中数学北师大版八年级下册第一章第一节第2课时 等边三角形的性质 同步练习
试卷更新日期：2022-02-15 类型：同步测试
一、单选题
-
1. 如图，正方形ABCD外侧作等边三角形ADE，则∠AEB的度数为（ ）
A、30° B、20° C、15° D、10°2. 等边三角形的两条中线相交所成的锐角为（ ）A、 B、 C、 D、3. 若a，b，c分别是 ABC的三边长，且满足a2﹣2ab+b2＝0，b2﹣c2＝0，则 ABC的形状是（ ）A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形4. 如图， 是等边三角形，两个锐角都是 的三角尺的一条直角边在 上，则 的度数为（ ）
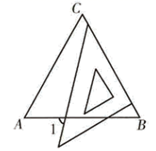A、 B、 C、 D、5. 下列命题中：1）两个全等三角形合在一起是一个轴对称图形；2）等腰三角形的对称轴是底边上的中线；3）等边三角形一边上的高就是这边的垂直平分线；4）一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形.正确的说法有（ ）A、1个 B、2个 C、3个 D、4个6. 如图所示，为线段上一动点（不与点 ， 重合），在同侧分别作正和正 ， 与交于点 ， 与交于点 ， 与交于点 ， 连接 ． 以下四个结论：①；②；③；④是等边三角形．其中正确的是（ ）
A、①②③④ B、②③④ C、①③④ D、①②③7. 如图，已知∠MON＝30°，点A1、A2、A3…在射线N上，点B1、B2、B3……在射线OM上；△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形若OA1＝1，则△A2020B2020A2021的边长（ ）
A、22019 B、4040 C、4038 D、22020二、填空题
-
8. 如图，△ABC是等边三角形，延长BC到点D，使CD＝AC，连接AD.则 .
9. 如图，将△ABC绕点A顺时针旋转60°得到△AED，若线段AB=3，则BE=.
10. 如图，在一个池塘两旁有一条笔直小路（B，C为小路端点）和一棵小树（A为小树位置）测得的相关数据为： 米，则 米.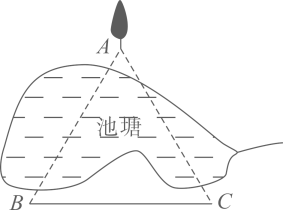
11. 等边三角形的边长为4，则其面积为.12. 如图，等边△ABC的边长为6，AD是高，F是边AB上一动点，E是AD上一动点，则BE+EF的最小值为.
13. 如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论中正确的有（填序号）①△BPQ是等边三角形②△PCQ是直角三角形③∠APB＝150° ④∠APC＝120°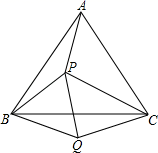
三、解答题
-
14. 如图，△ABC是等边三角形，D、E在边AB、AC的延长线上，且DEBC，分别交AB，AC于点D，E.求证：△ADE是等边三角形.
15. 如图， 是等边三角形， 是中线，延长 至E，使 ．求证： ．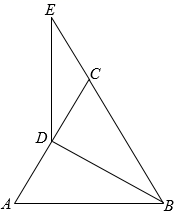
16. 货轮在海上以每小时6海里的速度沿南偏东40°的方向航行，已知货轮在B处时，测得灯塔A在其北偏东80°的方向上，航行半小时后货轮到达C处，此时测得灯塔A在其北偏东20°的方向上，求货轮到达C处时与灯塔A的距离.
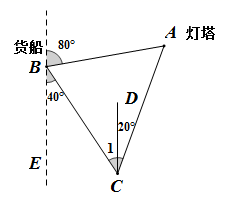17. 如图，四边形ABCD是正方形， ABE是等边三角形，M为对角线BD（不含B、D点）上任意一点，将线段BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．求证：AM=EN．
18. 如图，已知等边△ABC边长为1，D是△ABC外一点且∠BDC=120°，BD=CD，∠MDN=60°求△AMN的周长.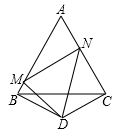
19. 如图
[感知]如图①，△ABC是等边三角形，点D、E分别在AB、BC边上，且AD=BE，易知：△ADC≌△BEA
(1)、[探究]如图②，△ABC是等边三角形，点D、E分别在边BA、CB的延长线上，且AD=BE，△ADC与△BEA还全等吗？如果全等，请证明：如果不全等，请说明理由．(2)、[拓展]如图③，在△ABC中，AB=AC，∠1=∠2，点D、E分别在BA、FB的延长线上，且AD=BE=CF，若AF=2AD，S△ABF=6，则S△BCD的大小为四、综合题
-
20. 如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC ， ∠OCD＝60°，连接OD ．
(1)、求证：△OCD是等边三角形；(2)、当α＝150°时，试判断△AOD的形状，并说明理由；(3)、当α＝时，△AOD是等腰三角形．