初中数学北师大版八年级下册第一章第一节第1课时 三角形的全等和等腰三角形的性质 同步练习
试卷更新日期:2022-02-15 类型:同步测试
一、单选题
-
1. 如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需加上条件( )
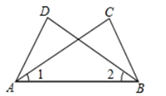 A、AD =BC B、BD=AC C、∠D=∠C D、OA=OB2. 已知如图,要测量水池的宽 ,可过点A作直线 ,再由点C观测,在 延长线上找一点 ,使 ,这时只要测量出 的长,就知道 的长,那么判定 的理由是( )
A、AD =BC B、BD=AC C、∠D=∠C D、OA=OB2. 已知如图,要测量水池的宽 ,可过点A作直线 ,再由点C观测,在 延长线上找一点 ,使 ,这时只要测量出 的长,就知道 的长,那么判定 的理由是( ) A、 B、 C、 D、3. 如图,在△ABC和△BAD中,已知∠CAB=∠DBA,添加下列条件,还不一定能判定△ABC≌△BAD的是( )
A、 B、 C、 D、3. 如图,在△ABC和△BAD中,已知∠CAB=∠DBA,添加下列条件,还不一定能判定△ABC≌△BAD的是( ) A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM4. 如图,△ABC≌△AED , 点E在线段BC上,∠1=44°,则∠AED的大小为( )
A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM4. 如图,△ABC≌△AED , 点E在线段BC上,∠1=44°,则∠AED的大小为( ) A、70° B、68° C、64° D、62°5. 等腰三角形的底角等于50°,则该等腰三角形的顶角度数为( )A、50° B、80° C、65°或50° D、50°或80°6. 等腰三角形的两边长分别是 和 ,则它的周长是( )A、 B、 C、 或 D、以上都不对7. 若中刚好有 ,则称此三角形为“可爱三角形”,并且 称作“可爱角”.现有 一个“可爱且等腰的三角形”,那么聪明的同学们知道这个三角形的“可爱角”应该是( ).A、或 B、或 C、或 D、或或8. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CD=AE.若BD=8,CD=5,则△DCG的面积是( )
A、70° B、68° C、64° D、62°5. 等腰三角形的底角等于50°,则该等腰三角形的顶角度数为( )A、50° B、80° C、65°或50° D、50°或80°6. 等腰三角形的两边长分别是 和 ,则它的周长是( )A、 B、 C、 或 D、以上都不对7. 若中刚好有 ,则称此三角形为“可爱三角形”,并且 称作“可爱角”.现有 一个“可爱且等腰的三角形”,那么聪明的同学们知道这个三角形的“可爱角”应该是( ).A、或 B、或 C、或 D、或或8. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CD=AE.若BD=8,CD=5,则△DCG的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,两个三角形全等,则∠α的度数是
 10. 如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上块,其理由是 .
10. 如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上块,其理由是 . 11. 如图,AB∥CD,点E在线段AC上,AB=AE.若∠ACD=38°,则∠1的度数为.
11. 如图,AB∥CD,点E在线段AC上,AB=AE.若∠ACD=38°,则∠1的度数为. 12. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是 °.
12. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是 °.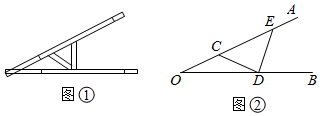 13. 如图,在△ABC中,AD⊥BC于点D , BD=DC , 若BC=6,AD=7,则图中阴影部分图形的面积为 .
13. 如图,在△ABC中,AD⊥BC于点D , BD=DC , 若BC=6,AD=7,则图中阴影部分图形的面积为 . 14. 如图,等腰△ABC中,AB=AC=5,BC=6,BD⊥AC,则BD=.
14. 如图,等腰△ABC中,AB=AC=5,BC=6,BD⊥AC,则BD=. 15. 如图,△PBC的面积为5cm2 , BP平分∠ABC,AP⊥BP于点P,则△ABC的面积为cm2 .
15. 如图,△PBC的面积为5cm2 , BP平分∠ABC,AP⊥BP于点P,则△ABC的面积为cm2 . 16. 如图, 中, , , ,点M从A点出发沿 路径向终点运动,终点为B点,点N从B点出发沿 路径向终点运动,终点为A点,点M和N分别以每秒 和 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作 于E, 于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为.
16. 如图, 中, , , ,点M从A点出发沿 路径向终点运动,终点为B点,点N从B点出发沿 路径向终点运动,终点为A点,点M和N分别以每秒 和 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作 于E, 于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为.
三、解答题
-
17. 如图,AB=AC,点D、E分别在AB、AC上,AD=AE,求证:CD=BE.
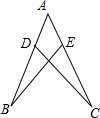 18. 已知:如图,在 中, ,D是BC的中点, , ,E , F是垂足, 吗?请说明理由.
18. 已知:如图,在 中, ,D是BC的中点, , ,E , F是垂足, 吗?请说明理由. 19. 如图,在 中, .分别延长 至点 使 ,连接 求 的度数.
19. 如图,在 中, .分别延长 至点 使 ,连接 求 的度数. 20. 如图,在△ABC中,AD BC,垂足是D,∠B=2∠C.求证:AB+BD= DC.
20. 如图,在△ABC中,AD BC,垂足是D,∠B=2∠C.求证:AB+BD= DC.
四、综合题
-
21. 已知:如图,已知 , , 和 相交于点 ,点 是 的中点,连接 .
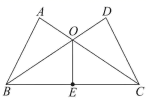 (1)、求证: ;(2)、求 的度数.22. 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转得到△AED,且点D在边BC上.
(1)、求证: ;(2)、求 的度数.22. 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转得到△AED,且点D在边BC上.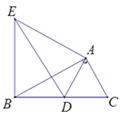 (1)、若∠DAC=50°,则∠ABE=度;(2)、求证:BE⊥BC:(3)、若点D是BC的中点,AC=2,求BE的值.
(1)、若∠DAC=50°,则∠ABE=度;(2)、求证:BE⊥BC:(3)、若点D是BC的中点,AC=2,求BE的值.


