初中数学浙教版2021-2022学年八年级下册3.1 平均数 同步测试
试卷更新日期：2022-02-14 类型：同步测试
一、单选题
-
1. 若一组数据3、4、5、x、6、7的平均数是5，则x的值是（ ）A、4 B、5 C、6 D、72. 已知一组数据的平均数为3，则数据的平均数是（ ）A、3 B、5 C、6 D、73. 某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表：
项目
作品
甲
乙
丙
丁
创新性
90
95
90
90
实用性
90
90
95
85
如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（ ）
A、甲 B、乙 C、丙 D、丁4. 小明随机抽查了九年级（2）班9位同学一周写数学作业的时间，分别为6，4，6，5，6，7，6，6，8（单位：h）.则估计本班大多数同学一周写数学作业的时间约为（ ）A、4h B、5h C、6h D、7h5. 某中学规定学生的学期体育成绩满分100分，其中课外体育占20％，期中考试成绩占30％，期末考试成绩占50％．小彤的三项成绩（百分制）依次为95，90，94，则小彤这学期的体育成绩为（ ）A、89 B、90 C、92 D、936. 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分（ ）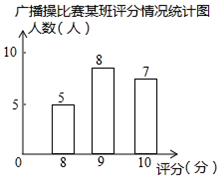
A、9 B、6.67 C、9.1 D、6.747. 某班在开展“节约每一滴水”的活动中，从全班40名同学中选出10名同学汇报了各自家庭一个月的节水情况，发现节水0.5m3的有2人，水1m3的有3人，节水1.5m3的有2人，节水2m3的有3人，用所学的统计知识估计全班同学的家庭一个月节约用水的总量是（ ）A、20m3 B、52m3 C、60m3 D、100m38. 某商场销售A ， B ， C ， D四种商品，它们的单价依次是50元，30元，20元，10元．某天这四种商品销售数量的百分比如图所示，则这天销售的四种商品的平均单价是（ ）
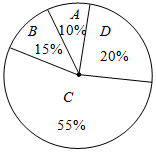A、19.5元 B、21.5元 C、22.5元 D、27.5元9. 某校评选先进班集体，从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分，各项满分均为 ，所占比例如下表：项目
学习
卫生
纪律
活动参与
所占比例
八年级 班这四项得分依次为 ， ， ， ，则该班四项综合得分（满分 ）为（ ）
A、 B、 C、 D、10. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（ ）A、20 B、18 C、15 D、14二、填空题
-
11. 某学校欲招聘一名教师，对应聘者甲进行了笔试和面试，其笔试和面试的成绩分别为80分和90分，若按笔试成绩占30%，面试成绩占70%计算综合成绩，则甲的综合成绩为分.12. 某学校八年级举行四科（含语文、数学、英语、物理四科）综合能力比赛，四科的满分都为100分，甲、乙、丙三人四科的测试成绩如下表：
学科
语文
数学
英语
物理
甲
95
85
85
60
乙
80
80
90
80
丙
70
90
80
95
综合成绩按照语文、数学、英语、物理四科测试成绩的1.2：1：1：0.8的比例计分，则丙的平均成绩为 ．
13. 某商场为了招聘商品拆装上架员工一名，设置了计算机、语言和商品知识三项测试，并对这三项测试成绩按照2：3：5的比确定.若某应试者三项测试成绩分别为70，50，80，则该应试者的平均成绩是.14. 学校将平时成绩、期中成绩和期末成绩按3∶3∶4计算学生的学期平均成绩．若某同学的数学平时成绩、期中成绩和期末成绩分别是90分、85分、90分，则该同学数学学期平均成绩是分．15. 某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此实际平均数与求出的平均数的差为 ．16. 为了解某校学生的睡眠情况，该校数学小组随机调查了部分学生一周的平均每天睡眠时间，设每名学生的平均每天睡眠时间为x时，共分为四组：A.6≤x＜7，B.7≤x＜8，C.8≤x＜9，D.9≤x≤10，将调查结果绘制成如图两幅不完整的统计图．（注：学生的平均每天睡眠时间不低于6时且不高于10时．）若该校有1500名学生，根据抽样调查结果，请估计该校平均每天睡眠时间低于8时的学生有 人．
三、解答题
-
17. 某公司招聘一名部门经理，对A、B、C三位候选人进行了三项测试，成绩如下（单位：分）：
候选人
语言表达
微机操作
商品知识
A
60
80
70
B
50
70
80
C
60
80
65
如果语言表达、微机操作和商品知识的成绩按3∶3∶4计算，那么谁将会被录取？
18. 在某希望实验中学七（8）班的体育课上，体育老师宣布了50米往返“运球”比赛规则，若规定30秒为达标成绩，现对其中一小组学生的成绩记录如下（超过30秒记为正，反之记为负）人数（人）
2
2
1
1
1
3
成绩（秒）
＋3
－2
0
＋1
＋7
－1
(1)、请计算这一小组学生的平均成绩.(2)、该小组达标率是多少？19. 台州某校七（1）班同学分三组进行数学活动，对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
七年级同学最喜欢喝的饮料种类情况统计图
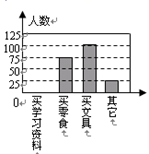
八年级同学零花钱最主要用途情况统计图
九年级同学完成家庭作业时间情况统计表
时间
1小时左右
1.5小时左右
2小时左右
2.5小时左右
人数
50
80
120
50
根据以上信息，请回答下列问题：
(1)、七年级400名同学中最喜欢喝“冰红茶”的人数是多少？(2)、补全八年级300名同学中零花钱的最主要用途情况频数分布直方图；(3)、九年级300名同学中完成家庭作业的平均时间大约是多少小时（结果保留一位小数）？20. 某校举办七年级数学素养大赛，比赛共设三个项目：速算比赛、数学推理、巧解方程，每个项目得分都按一定百分比折算后计入总分。甲、乙、丙三位同学的速算比赛得分均为85分，且此项在总分中所占百分比不变，其余两项得分如下图所示(单位：分)。
(1)、根据图中信息判断哪位同学总分得分最低？(2)、甲、丙两同学的数学推理与巧解方程两项经折算后的得分和均为52分，求这两项在计入总分时所占的百分比；(3)、写出三个项目各项所占百分比的一组值，使甲或丙同学能获得第一名。21. 某公司想招聘一名新职员，对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核，他们的各项得分（百分制，单位：分）如表所示：应试者
面试成绩
笔试成绩
才艺
甲
86
79
90
乙
84
81
75
丙
80
90
73
(1)、请通过计算三项得分的平均分，从低到高确定应聘者的排名顺序；(2)、公司规定：面试、笔试、才艺得分分别不得低于80分、80分、70分，并按照50%、40%、10%的比例计入个人总分，请你确定谁会被录用？并说明理由．
22. 某公司计划从内部选拔一名管理人员，先对甲、乙、丙三名候选人进行了笔试、面试两项测试，三人的测试成绩如下表；该公司再组织200名职工利用投票推荐的方式对这三人进行了民主评议，三人得票见扇形统计图（没有弃权票，每位职工只能推荐1人，每得1票记作1分．）测试项目
测试成绩/分
甲
乙
丙
笔试
69
80
92
面试
95
80
72
(1)、请计算出甲、乙、丙三名候选人的民主评议得分；(2)、根据实际需要，单位将笔试、面试、民主评议三项得分按5：3：2的比例确定个人成绩，那么谁将被录用？23. 对于三个实数a，b，c，用 表示这三个数的平均数，用min 表示这三个数中最小的数.例如： ，min ，min .请结合上述材料，解决下列问题：
(1)、 ；(2)、若min ，则整数 的值是；(3)、若 min ，求 的值.24. 如图是某厂对一批电灯泡的使用寿命进行检测后得到的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）.组别（时）
频数
400～450
20
450～500
m
500～550
30
550～600
10
(1)、求m的值.(2)、若一个电灯泡亮一小时耗电0.1度，则这批电灯泡的总耗电量会超过5200度吗？说明理由.