2022年高考数学二轮复习 解答题型 26 概率与统计

试卷更新日期：2022-02-14 类型：二轮复习

进入 出卷网 下载

一、解答题

  • 1. 在“十三五”期间，我国的扶贫工作进入了“精准扶贫”阶段，到2020年底，全国830个贫困县全部脱贫摘帽，最后4335万贫困人口全部脱贫，这是我国脱贫攻坚史上的一大壮举．重庆市奉节县作为国家贫困县之一，于2019年4月顺利脱贫摘帽，因地制宜发展特色产业，是奉节脱贫攻坚的重要抓手．奉节县规划发展了以高山烟叶、药材、反季节蔬菜；中山油橄榄、养殖；低山脐橙等为主的产业格局，各类特色农产品已经成为了当地村民的摇钱树．尤其是奉节脐橙，因“果皮中厚、脆而易剥，肉质细嫩化渣、无核少络，酸甜适度，汁多爽口，余味清香”而闻名．为了防止返贫，巩固脱贫攻坚成果，各职能部门对脐橙种植、销售、运输、改良等各方面给予大力支持．奉节县种植的某品种脐橙果实按果径X（单位：mm）的大小分级，其中X∈(70 ， 90]为一级果，X∈(90 ， 110]为特级果，一级果与特级果统称为优品．现采摘了一大批此品种脐橙果实，从中随机抽取1000个测量果径，得到频率分布直方图如下：

    参考数据：若随机变量X服从正态分布N(μ ， σ2) ， 则P(μ−σ<X≤μ+σ)≈0.6827 ， P(μ−2σ<X≤μ+2σ)≈0.9545 ， P(μ−3σ<X≤μ+3σ)≤0.9973 ．

    (1)、由频率分布直方图可认为，该品种脐橙果实的果径X服从正态分布N(μ ， σ2) ， 其中μ近似为样本平均数x¯ ， σ近似为样本标准差s，已知样本的方差的近似值为100．若从这批脐橙果实中任取一个，求取到的果实为优品的概率（同一组中的数据用该组区间的中点值代表）
    (2)、这批采摘的脐橙按2个特级果和n（n≥2 ， 且n∈N*）个一级果为一箱的规格进行包装，再经过质检方可进入市场．质检员质检时从每箱中随机取出两个果实进行检验，若取到的两个果实等级相同，则该箱脐橙记为“同”，否则该箱脐橙记为“异”．

    ①试用含n的代数式表示抽检的某箱脐橙被记为“异”的概率p；

    ②设抽检的5箱脐橙中恰有3箱被记为“异”的概率为f(p) ， 求函数f(p)的最大值，及取最大值时n的值．

    查看试题解析

  • 2. 手机支付也称为移动支付，是指允许用户使用其移动终端（通常是手机）对所消费的商品或服务进行账务支付的一种服务方式．随着信息技术的发展，手机支付越来越成为人们喜欢的支付方式．某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查，随机抽取了100人，其年龄频率分布表和使用手机支付的人数如下所示：（年龄单位：岁）

    年龄段

    [15，25）

    [25，35）

    [35，45）

    [45，55）

    [55，65）

    [65，75]

    频率

    0.1

    0.32

    0.28

    0.22

    0.05

    0.03

    使用人数

    8

    28

    24

    12

    2

    1

    参考公式：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d) ．

    (1)、若以45岁为分界点，根据以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关？


    年龄低于45岁

    年龄不低于45岁

    使用手机支付

    不使用手机支付

    (2)、若从年龄在[55，65），[65，75]的样本中各随机选取2人进行座谈，记选中的4人中“使用手机支付”的人数为X，求随机变量X的分布列和数学期望．

    参考数据：

    P（K2≥k0）

    0.025

    0.010

    0.005

    0.001

    k0

    3.841

    6.635

    7.879

    10.828

    查看试题解析

  • 3. 书籍是精神世界的人口，阅读让精神世界闪光，阅读已成为中学生的一种生活习惯，每年4月23日为世界读书日．某研究机构为了解某地中学生的阅读情况，通过随机抽样调查了n名中学生，对这些人每周的平均阅读时间（单位：小时）进行统计，并将样本数据分成[0，2），[2，4），[4，6），[6，8），[8，10），[10，12），[12，14），[14，16），[16，18]九组，绘制成如图所示的频率分布直方图．已知这n名中学生中每周平均间读时间不低于16小时的人数是2人．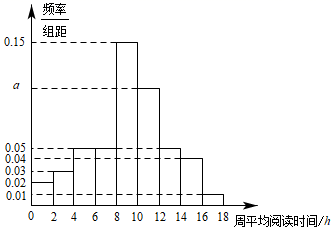

    (1)、求n和a的值；
    (2)、为进一步了解这n名中生数字媒体读时间和纸质图书阅读时间的分配情况，从周平均时间在[8，10），[10，12），[12，14）三组内的学生中，采用分层抽样的方法抽取了6人，现从这6人中随机抽取3人，记周平均阅读时间在[10，12）内的中学生人数为X，求X的分布列和数学期望．

    查看试题解析

  • 4. 某机构为了解市民对交通的满意度，随机抽取了100位市民进行调查结果如下：回答“满意”的人数占总人数的一半，在回答“满意”的人中，“上班族”的人数是“非上班族”人数的37；在回答“不满意”的人中，“非上班族”占15.

    附：

    α

    0.1

    0.05

    0.01

    0.005

    0.001

    x0

    2.706

    3.841

    6.635

    7.879

    10.828

    参考公式：x2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d) ， 其中n=a+b+c+d.

    (1)、请根据以上数据填写下面2×2列联表，并依据小概率值α=0.001的独立性检验，分析能否认为市民对于交通的满意度与是否为上班族存关联？


    满意

    不满意

    合计

    上班族

    非上班族

    合计

    (2)、为了改善市民对交通状况的满意度，机构欲随机抽取部分市民做进一步调查.规定：抽样的次数不超过n(n∈N+) ， 若随机抽取的市民属于不满意群体，则抽样结束；若随机抽取的市民属于满意群体，则继续抽样，直到抽到不满意市民或抽样次数达到n时，抽样结束.

    （i）若n=5 ， 写出X5的分布列和数学期望；

    （ii）请写出Xn的数学期望的表达式（不需证明），根据你的理解说明Xn的数学期望的实际意义.

    查看试题解析

  • 5. 2014年，中央和国务院办公厅印发《关于引导农村土地经营权有序流转发展农业适度规模经营的意见》，要求大力发展土地流转和适度规模经营.某种粮大户2017年开始承包了一地区的大规模水田种植水稻，购买了一种水稻收割机若干台，这种水稻收割机随着使用年限的增加，每年的养护费也相应增加，这批水稻收割机自购买使用之日起，5年以来平均每台水稻收割机的养护费用数据统计如下：

    年份

    2017

    2018

    2019

    2020

    2021

    年份代码x

    1

    2

    3

    4

    5

    养护费用y（万元）

    1.1

    1.6

    2

    2.5

    2.8

    参考数据：∑i=15yi=10 ， ∑i=13xyi=34.3 ， ∑i=13xi2=55.参考公式：回归直线的斜率和截距的最小二乘法估计公式分别为：b=∑i=1nxiyi−n⋅x⋅y∑i=1nxi2−n⋅x2 ， a=y−bx.

    (1)、求y关于x的线性回归方程；
    (2)、若该水稻收割机的购买价格是每台16万元，由（1）中的回归方程，从每台水稻收割机的年平均费用角度，你认为一台该水稻收割机是使用满5年就淘汰，还是继续使用到满8年再淘汰？

    查看试题解析

  • 6. 已知甲、乙、丙三个研究项目的成员人数分别为20，15，10．现采用分层抽样的方法从中抽取9人，进行睡眠时间的调查．
    (1)、应从甲、乙、丙三个研究项目的成员中分别抽取多少人？
    (2)、若抽出的9人中有4人睡眠不足，5人睡眠充足，现从这9人中随机抽取3人做进一步的访谈调研，若随机变量X表示抽取的3人中睡眠充足的成员人数，求X的分布列与数学期望．

    查看试题解析

  • 7. 甲、乙两所学校之间进行排球比赛，采用五局三胜制(先赢3局的学校获胜，比赛结束)，约定比赛规则如下：先进行男生排球比赛，共比赛两局，后进行女生排球比赛，直到分出胜负．按照以往比赛经验，在男生排球比赛中，每局甲校获胜的概率为23 ， 乙校获胜的概率为13 ， 在女生排球比赛中，每局甲校获胜的概率为13 ， 乙校获胜的概率为23 ， 每局比赛结果相互独立．
    (1)、求甲校以3：1获胜的概率；
    (2)、记比赛结束时女生比赛的局数为ξ ， 求ξ的分布列及期望．

    查看试题解析

  • 8. 某土特产超市为预估2022年元旦期间游客购买土特产的情况，对2021年元旦期间的90位游客购买情况进行统计，得到如下人数分布表：

    购买金额（元）

    [0，150）

    [150，300）

    [300，450）

    [450，600）

    [600，750）

    [750，900]

    人数

    10

    15

    20

    15

    20

    10

    附：参考公式和数据：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d) ， n=a+b+c+d.

    附表：

    k0

    2.072

    2.706

    3.841

    6.635

    7.879

    P(K2≥k0)

    0.150

    0.100

    0.050

    0.010

    0.005

    (1)、根据以上数据完成2×2列联表，并判断是否有95%的把握认为购买金额是否少于600元与性别有关．


    不少于600元

    少于600元

    合计

    男

    40

    女

    18

    合计

    (2)、为吸引游客，该超市推出一种优惠方案：购买金额不少于600元可抽奖3次，每次中奖概率为P（每次抽奖互不影响，且P的值等于人数分布表中购买金额不少于600元的频率），中奖1次减50元，中奖2次减100元，中奖3次减150元．若游客甲计划购买800元的土特产，请列出实际付款数X（元）的分布列并求其数学期望．

    查看试题解析

  • 9. 为了应对国家电网用电紧张的问题，了解我市居民用电情况，我市统计部门随机调查了200户居民去年一年的月均用电量（单位：kW·h），并将得到数据按如下方式分为9组：[0，40），[40，80），…，[320，360]，绘制得到如下的频率分布直方图：

    (1)、试估计抽查样本中用电量在[160，200）的用户数量；
    (2)、为了解用户的具体用电需求，统计部门决定在样本中月均用电量为[0，40）和[320，360]的两组居民用户中随机抽取两户进行走访，求走访对象来自不同的组的概率．

    查看试题解析

  • 10. 为了了解学生参加体育活动的情况，某校对学生进行了随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少”，共有4个选项可供选择（    ）

    A.1.5小时以上 B.1~1.5小时 C.0.5~1小时 D.0.5小时以下

    下图是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题.

    (1)、求本次一共调查了多少名学生，并在图①中将选项B对应的部分补充完整；
    (2)、采用分层抽样的方法在C组和D组中共抽取8人，求C组，D组各抽取的人数；
    (3)、在（2）中抽取的8人中采用简单随机抽样的方法抽取2人，求这2人中至少有1人来自D组的概率.

    查看试题解析

  • 11. 新型冠状病毒肺炎，简称“新冠肺炎”，是指2019新型冠状病毒感染导致的肺炎．某定点医院对来院就诊的发热病人的血液进行检验，随机抽取了1000份发热病人的血液样本，其中感染新型冠状病毒的有200份，以频率作为概率的估计值．
    (1)、某时间段内来院就诊的5名发热病人中，恰有3人感染新型冠状病毒的概率是多少？
    (2)、治疗重症病人需要使用呼吸机，若该呼吸机的一个系统G由3个电子元件组成，各个电子元件能否正常工作的概率均为12 ， 且每个电子元件能否正常工作相互独立．若系统G中有超过一半的电子元件正常工作，则G可以正常工作．为提高G系统正常工作概率，在系统内增加两个功能完全一样的其他品牌的电子元件，每个新元件正常工作的概率均为p（0<P<1），且新增元件后有超过一半的电子元件正常工作，则G可以正常工作，问：p满足什么条件时，可以提高整个G系统的正常工作概率？

    查看试题解析

  • 12. COP15大会原定于2020年10月15~28日在昆明举办，受新冠肺炎疫情影响，延迟到今年10月11~24日在云南昆明举办，同期举行《生物安全议定书》､《遗传资源议定书》缔约方会议.为助力COP15的顺利举行，来自全省各单位各部门的青年志愿者们发扬无私奉献精神，用心用情服务，展示青春风采.会议期间有两家外卖公司帮部分志愿者送餐，送餐员的工资方案如下：A公司的底薪40，每单抽成4元；B公司无底薪，40单以内（含40单）的部分每单抽成5元，超出40单的部分每单抽成6元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其80天的送餐单数，得到如下频数表：

    A公司送餐员送餐单数频数表：

    送餐单数

    37

    38

    39

    42

    43

    天数

    20

    25

    10

    15

    10

    B公司送餐员送餐单数频数表：

    送餐单数

    37

    38

    39

    42

    43

    天数

    10

    20

    20

    25

    5

    若将频率视为概率，回答下列两个问题：

    (1)、记B公司送餐员日工资为X（单位：元），求X的分布列和数学期望；
    (2)、小李打算到A ， B两家公司中的一家应聘送餐员，如果仅从日工资的角度考虑，小张应选择哪家公司应聘？请说明你的理由.

    查看试题解析

  • 13. 2021年7月18日第 30 届全国中学生生物学竞赛在浙江省萧山中学隆重举行．为做好本次考试的评价工作，将本次成绩转化为百分制，现从中随机抽取了50名学生的成绩，经统计，这批学生的成绩全部介于40至100之间，将数据按照 [40 ， 50) ， [50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100] 分成 6 组，制成了如图所示的频率分布直方图．

    (1)、求频率分布直方图中 m 的值，并估计这50名学生成绩的中位数；
    (2)、在这50名学生中用分层抽样的方法从成绩在， [70 ， 80) ， [80 ， 90) ， [90 ， 100] 的三组中抽取了11人，再从这11人中随机抽取3人，记 ξ 的分布列和数学期望；
    (3)、转化为百分制后，规定成绩在 [90 ， 100] 的为A等级，成绩在 [70 ， 90) 的为 B 等级，其它为 C 等级．以样本估计总体，用频率代替概率，从所有参加生物竞赛的同学中随机抽取100人，其中获得 B 等级的人数设为 η ，记 B 等级的人数为 k 的概率为 P(η=k) ，写出 P(η=k) 的表达式，并求出当 k 为何值时， P(η=k) 最大？

    查看试题解析

  • 14. 平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定：所有主干道路凡机动车途经十字口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以100元罚款，记\text{3}分的行政处罚．如表是本市一主干路段监控设备所抓拍的5个月内，机动车驾驶员不“礼让斑马线”行为统计数据：

    月份

    1

    2

    3

    4

    5

    违章驾驶员人数

    120

    105

    100

    90

    85.

    （Ⅰ）请利用所给数据求违章人数y与月份x之间的回归直线方程y^=b^x+a^；

    （Ⅱ）预测该路段7月份的不“礼让斑马线”违章驾驶员人数．

    参考公式：b^=∑i=1nxiyi−nxy¯∑i=1nxi2−nx¯2=∑i=1n(xi−x)(yi−y¯)∑i=1n(x−x)2 ， a^=y¯−b^x¯ ．

    查看试题解析

  • 15. 某城市100户居民的月平均用电量（单位：千瓦时）以 [160 ， 180) ， [180 ， 200) ， [200 ， 220) ， [220 ， 240) ， [240 ， 260) ， [260 ， 280) ， [280 ， 300] 分组的频率分布直方图如图.

    (1)、求直方图中 x 的值；
    (2)、求月平均用电量的众数和中位数；
    (3)、在月平均用电量为 [240 ， 260) ， [260 ， 280) ， [280 ， 300] 的三组用户中用分层抽样的方法抽取6户居民，并从抽取的6户中任选2户参加一个访谈节目，求参加节目的2户来自不同组的概率.

    查看试题解析

  • 16. 国际学生评估项目（PISA），是经济合作与发展组织（OECD）举办的，该项目的内容是对15岁学生的阅读、数学、科学能力进行评价研究．在2018年的79个参测国家（地区）的抽样测试中，中国四省市（北京、上海、江苏、浙江作为一个整体在所有参测国家（地区）取得全部3项科目中第一的好成绩，某机构为了分析测试结果优劣的原因，从参加测试的中国学生中随机抽取了200名参赛选手进行调研，得到如下统计数据：

    成绩优秀

    成绩一般

    总计

    家长高度重视学生教育

    90

    x

    y

    家长重视学生教育度一般

    30

    z

    ω

    总计

    120

    80

    200

    若从上表“家长高度重视学生教育”的参测选手中随机抽取一人，则选到的是“成绩一般”的选手的概率为 413 ．

    附 K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d) ， n=a+b+c+d ．

    (PK2≥k0)

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828
    (1)、判断是否有99.9%的把握认为“学生取得的成绩情况”与“家长对学生的教育重视程度”有关；
    (2)、现从成绩优秀的选手中按照分层抽样的方法抽取20人．进行“家长对学生情感支持”的调查，再从这20人中抽取3人进行“学生家庭教育资源保障”的调查．记进行“学生家庭教育资源保障”调查中抽取到“家长高度重视学生教育”的人数为X，求X的分布列和数学期望．

    查看试题解析