浙江省衢州市开化县2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-02-14 类型：期末考试

进入出卷网下载

一、选择题（本大题共有8小题，每小题3分，共24分．)

1. 下列图案中，成轴对称图形的是（ )

A、 B、 C、 D、

查看试题解析
2. 如果一个三角形的两边长分别为2和5，则第三边长可能是（　　）

A、2 B、3 C、5 D、8

查看试题解析
3. 已知点P的坐标为(-2，3)，则点P到y轴的距离为（）

A、2 B、3 C、5 D、 $\sqrt{13}$

查看试题解析
4. 已知 a，b都是实数，且a<b，则下列不等式的变形正确的是（ )

A、a-1>b-1 B、-a+2<-b+2 C、3a<3b D、 $\frac{a}{2} > \frac{b}{3}$

查看试题解析
5. 如图，在△ABC中，AB=AC，∠A=36°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD等于（ )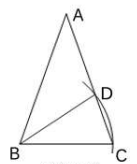

A、36° B、46° C、54° D、72°

查看试题解析
6. 已知点P(2-m，m-5)在第三象限，则整数m的值是（）

A、4 B、3，4 C、4，5 D、2，3，4

查看试题解析
7. 下列命题是真命题的是（ )

A、同旁内角互补 B、任意一个等腰三角形一定是钝角三角形 C、两边及一角对应相等的两个三角形全等 D、角平分线上的点到角两边的距离相等

查看试题解析
8. 如图，已知点K为直线I：y=2x+4上一点，先将点K向下平移2个单位，再向左平移a个单位至点K₁ ，然后再将点K₁向上平移b个单位，向右平1个单位至点K₂ ，若点K₂也恰好落在直线l上，则a，b应满足的关系是（ )

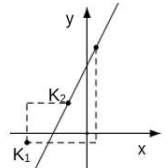A、a+2b=4 B、2a-b=4 C、2a+b=4 D、a+b=4

查看试题解析

二、填空题（本大题共有8小题，每小题3分，共24分)

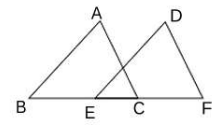
9. 不等式3x-1<5的解是.

查看试题解析
10. 已知正比例函数 $y = 3 x$ 的图象经过点 $(1, m)$ ，则 $m$ 的值为．

查看试题解析
11. 如图，在△ABC和△DEF中，∠B=∠DEF，∠A=∠D，请你添加一个条件，使△ABC≌△DEF（图形中不再增加其他字母）.

查看试题解析
12. 如图，△ABC是等边三角形.在AC，BC边上各取一点P，Q，使 AP=CQ，且∠ABP=20°，AQ，BP相交于点O，则∠AQB=.

查看试题解析
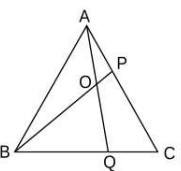13. 如图，一次函数y=2x和y=ax+5的图象交于点A(m，3)，则不等式ax+5<2x的解集是.

查看试题解析
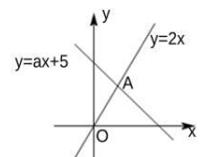14. 一次中学生宪法知识竞赛中共有20道题，每一题答对得5分，答错或不答都扣3分.若小丽答了所有的题，要想获得优胜奖（75分及以上)，则她至少要答对道题.

查看试题解析
15. 如图，在Rt△ABC中，∠C=90°，∠A=30°，分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧交于M，N两点，连结MN分别交 AB，AC于点E，D，若 AD=8，则AB的长为.

查看试题解析
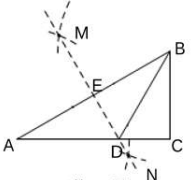16. 如图1，在 Rt△ABC中，∠C=90°，点P从点C出发，沿三角形的边以1cm/秒的速度顺时针运动一周，点P运动时线段CP的长度y (cm）随运动时间×(秒）变化的关系如图2所示，若点M的坐标为（11，5)，则点P运动一周所需要的时间为秒.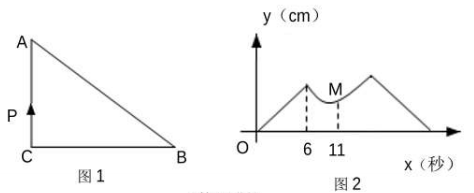

查看试题解析

三、解答题（本大题共有7小题，共52分.)

17. 解不等式组
${\begin{array}{l} 2 x + 4 ⩽ 3 (x + 2) \\ \frac{x - 1}{2} < 2 \end{array}$

查看试题解析
18. 如图，在4x4的方格纸中，请按要求画格点三角形（顶点在格点上).

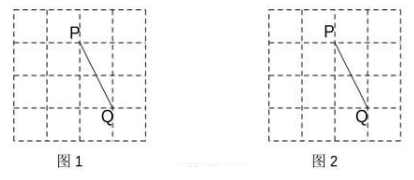(1)、在图1中画格点△PQO，使△PQO是以点P为直角顶点的等腰直角三角形.

(2)、在图2中画格点△QMN，使PQ是△QMN 的中线，且M，N不在同一条网格线上．

查看试题解析
19. 如图，在△ABC中，AB=AC，点D，E在BC上，BD=CE.

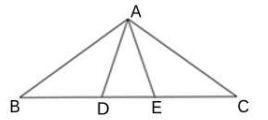(1)、求证：△ABD≌△ACE.

(2)、若∠DAE=∠B=28 °，求∠BAD的度数.

查看试题解析
20. 如图，在平面直角坐标系中，△ABC的顶点在网格的格点上.

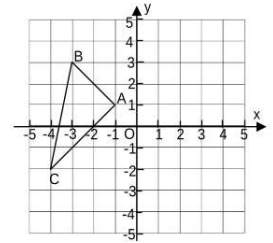(1)、写出点A，B的坐标：A ， B.

(2)、在图中作△ABC关于y轴对称的图形△A₁B₁C₁

(3)、求△ABC的面积.

查看试题解析
21. 为拓展学生视野，丰富学生的社会实践经验。某校计划组织师生共300人前往江山绿然滕农场开展研学活动，如果租用6辆大客车和5辆小客车恰好全部坐满．已知每辆大客车的乘客座位数比小客车多17个.

(1)、求每辆大客车和每辆小客车的乘客座位数；

(2)、由于最后参加活动的人数增加了30 人，学校决定调整租车方案．在保持租用车辆总数不变的情况下，为将所有参加活动的师生装载完成，求租用小客车数量的最大值.

查看试题解析
22. 如图1所示，甲，乙两车从 $A$ 地匀速出发，沿相同路线前往同一目的地，途中经过 $B$ 地.甲车先出发，当甲车到达 $B$ 地时，乙车开始出发.当乙车到达 $B$ 地时，甲车与 $B$ 地相距 $\frac{50}{3} k m$ .设甲，乙两车与 $B$ 地之间的距离分别为 $y_{1} (k m) ， y_{2} (k m)$ ，乙车行驶的时间为 $x (h) ， y_{1} ， y_{2}$ 与 $x$ 的函数关系如图2所示.

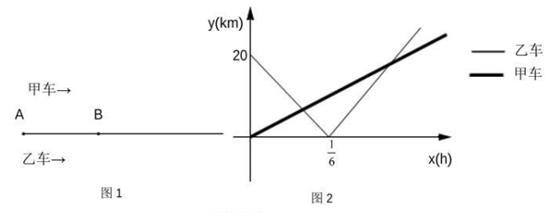(1)、求甲车和乙车的速度.

(2)、求 $y_{1} ， y_{2}$ 与 $x$ 的函数关系式.

(3)、当 $x$ 为何值时，甲、乙两车相距 $5 km$ ?

查看试题解析
23. 如图1，在△ABC，AB=AC=10，BC=12.

(1)、求BC边上的高线长.

(2)、点E是BC边上的动点，点D在边AB上，且AD=4，连结DE.
①如图2，当点E是BC中点时，求△BDE的面积.

②如图3，沿DE将△BDE折叠得到△FDE，当DF与△ABC其中一边垂直时，求BE的长.

查看试题解析