浙江省丽水市龙泉市2021-2022学年八年级上学期数学期末试卷
试卷更新日期：2022-02-14 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分)
-
1. 点P(3，4)在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下面垃圾分类的图标中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 若长度为a，2，5的三条线段能组成一个三角形，则a可以是（ ）A、2 B、3 C、4 D、74. 在一次函数y=2x-1图象上的点是（ ）A、(2，3) B、(0，1) C、(1，0) D、(-1，1)5. 不等式3x>6的解集在数轴上可表示为（ ）A、
B、
C、
D、
6. 下列命题中，是真命题的是（ ）A、对应角相等的两个三角形是全等三角形 B、三个内角之比为3∶4∶5的三角形是直角三角形 C、平面直角坐标系中，点的横坐标是点到x轴的距离 D、角平分线上的点到角两边的距离相等7. 某次知识竞赛一共有20道题，答对一题得5分，不答得0分，答错扣2分.小聪有1道题没答，竞赛成绩超过80分，则小聪至少答对的题数是（ ）A、15 B、16 C、17 D、188. 若直角三角形的两边长分别是5和12，则它的斜边长是（ ）A、13 B、13或 C、 D、12或139. 如图，等边△ABC的边长为4，点P在BC 上，连结AP.则△ABP的面积y与BP的长x的函数图象大致是（ ）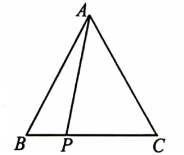
A、
B、
C、
D、
10. 如图，AB llCD，点E是AD上的点，连结 BE，CE，且∠BEC=90°，BE平分∠ABC.以下结论中：①E是AD中点，②AB+CD=BC，③AE=CE，④ 正确的个数为（ ）
A、4 B、3 C、2 D、1二、填空题(本题有6小题，每小题3分，共18分)
-
11. 若a<b，则3a3b(填“>”或“<").12. 函数y=kx(k为常数且k≠0)的图象经过点(2，4)，则k的值为.13. 如图，△ABC≌△DEF，若∠A=65° ，则∠EDC的度数为.
14. 若点P(-1，3)与点P'(a+1，3)关于y轴对称，则a为.15. 小明骑车回家过程中，骑行的路程s与时间t的关系如图所示.则经15分钟后小明离家的路程为.
16. 如图，在Rt△ABC中，∠ACB=90°，D为AB上异于A，B的一点，AC≠BC.
(1)、若D为AB中点，且 CD=2，则AB=.(2)、当CD= AB时，∠A=α ，要使点D必为AB的中点，则α的取值范围是.三、解答题(本题有8小题，第17~22题每题6分，第23~24题每题8分，共52分。)
-
17. 解下列一元一次不等式(组)．(1)、x-3＞5(2)、18. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A(4，3)，B(2，1)，C(3，0).将△ABC向左平移3个单位长度得到△A'BC.
(1)、作出△A'B'C′.(2)、写出点A'，B'，C′的坐标.19. 如图，在△ABC中，AD平分∠BAC.AB=AC=3，AD=2，求BC的长.
20. 已知一次函数的图象经过点A(0，3)，B(2，-3).(1)、求函数的表达式.(2)、若P(1，y1)，Q(3，y2)是该函数图象上的两点，试比较y1与y2的大小关系.21. 如图，点D，E分别在AC，AB上，AD=AE，BE=CD.
(1)、求证：BD=CE.(2)、若∠A=55° ，∠C=30°，求∠COD的度数.22. 某学校准备组织30名教师和若干名学生去“百山祖国家公园"开展研学活动，联系了甲、乙两家旅行社.经洽谈，两家旅行社的收费如下表所示：旅行社
收费标准
优惠
甲
100元/人
教师全额收费，学生按七五折收费
乙
100元/人
师生一律按八折收费
设参加研学活动的学生共有x人，甲、乙两家旅行社的费用分别为y甲、 y乙.
(1)、分别求y甲y乙关于x的函数表达式.(2)、问学校选择哪家旅行社付费较少?23. 如图是我国古代数学家赵爽创制的一副“勾股圆方图”(又称“赵爽弦图”)，它是由四个全等的直角三角形与中间的一个小正方形EFGH无缝拼成的大正方形ABCD.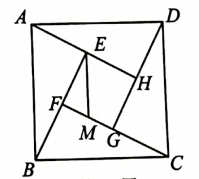
(1)、若 ，求AB(2)、点M在FG上， ，且 ，求正方形ABCD与正方形EFGH的周长比.24. 如图，直线y=kx+b与x轴交于点A(4.0).与y轴交于点B(0，2)，P是x轴上的动点.
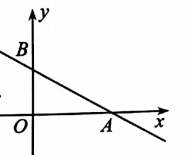(1)、求k的值.(2)、连结PB，当∠PBA=90°时，求OP的长.(3)、过点P作AB的平行线，交y轴于点M，点Q在直线x=2上.是否存在点Q，使得△PMQ是等腰直角三角形?若存在，请直接写出所有符合条件的点Q的坐标，若不存在，请说明理由.