浙江省嘉兴市2021-2022学年八年级上学期数学期末试卷

试卷更新日期：2022-02-14 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分)

1. 在下列交通标志图案中，属于轴对称图形的是（ )

A、 B、 C、 D、

查看试题解析
2. 如果一个三角形的两边长都是6cm，则第三边的长不能是（ )

A、3em B、6cm C、9cm D、13cm

查看试题解析
3. 平面直角坐标系中，点A(-1，3)到y轴的距离是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 小嘉去电影院观看《长津湖》，如果用(5，7)表示5排7座，那么小嘉坐在7排8座可表示为（ )

A、(5，7) B、(7，8） C、(8，7) D、(T，5)

查看试题解析
5. 如图，在△ABC中，∠ACB=90°，点D是AB的中点，连接CD，若AC=4，BC=3，则CD的长度是（ )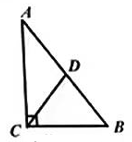

A、1.5 B、2 C、2.5 D、5

查看试题解析
6. 若a<b，c≠0，则下列不等式不一定成立的是（ )

A、 $a + c < b + c$ B、 $a - c < b - c$ C、 $a c^{2} < b c^{2}$ D、 $\frac{a}{c} < \frac{b}{c}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = A C ， A D$ 是BC边上的高，点 $E$ 在AD上，且 $A E = \frac{1}{3}$ ，则△ABC的面积为s，则是△ABE的面积是（）

A、 $\frac{S}{2}$ B、 $\frac{S}{3}$ C、 $\frac{S}{4}$ D、 $\frac{S}{6}$

查看试题解析
8. 如图，折叠直角三角形纸片ABC，使得点A、B都与斜边AB上的点F重合，折痕分别为DE和GH、则下列结论不一定成立的是（ )

A、 $D H = \frac{1}{2} A B$ B、 $E F = F G$ C、 $E F ⊥ F G$ D、 $D E / / G H$

查看试题解析
9. 已知点 $A (m - 1 ， y_{1})$ 和点 $B (m + 1 ， y_{2})$ 在一次函数 $y = (k + 2) x + 1$ 的图象上，且y₁>y₂ ，下列四个选项中k的值可能是（ )

A、-3 B、-1 C、1 D、3

查看试题解析
10. 如图，在等腰直角三角形ABC中， $∠ B A C = 90^{°}$ ，等边三角形ADE的顶点 $D$ 在BC边上，连接CE，已知 $∠ D C E = 90^{°} ， C D = \sqrt{2}$ ，则AB的长为（）

A、 $\sqrt{2}$ B、 $\sqrt{3} + 1$ C、 $2 \sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、填空题（本题有10小题，每小题3分，共30分)

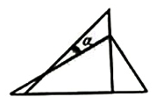
11. 根据数量关系“x的3倍小于4”，列不等式为.

查看试题解析
12. 若点A (5，m）是直线y= 2x 上一点，则m=.

查看试题解析
13. 命题“两个全等三角形的周长相等”的逆命题是.

查看试题解析
14. 将一副三角板按如图所示叠放在一起，则图中∠α的度数为.

查看试题解析
15. 在平面直角坐标系中，把点A(-1，-2)向右平移2个单位到点B，则点B位于第象限.

查看试题解析
16. 如图，在△ABC与△ACD中，ABllCD，请添加一个条件：，使△ABC≌△CDA.

查看试题解析
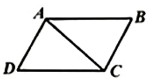17. 一次知识竞赛一共有26道题，答对一题得4分，不答得0分，答错一题扣2分，小明有1道题没答，竞赛成绩不少于88分，则小明至少答对题.

查看试题解析
18. 如图，在等边三角形ABC 中，BD是AC边上的中线，过点D作DE⊥BC于点E，若AB=2，则CE的长为.

查看试题解析
19. 如图，直线y = kx+1与直线y=-2x+b交于点A（1，2) ，由图象可知，不等式kx+1≥-2x +b的解为.

查看试题解析
20. 若一次函数y=ax+b（a≠0)的图象经过点A(2，3)，且不经过第四象限，则 4a+b的取值范围为.

查看试题解析

三、解答题(本题有6小题。第21~24题每题6分，第25、26题每题8分，共40分)

21. 解不等式3(x-1)≤9，并把解在数轴上表示出来.

查看试题解析
22. 如图，AD平分 $∠ B A C ， ∠ A D B = ∠ A D C$ .

(1)、求证： $△ A B D \subseteq △ A C D$ ：

(2)、若 $∠ B = 25^{°} ， ∠ B A C = 40^{°}$ ，求 $∠ B D C$ 的度数.

查看试题解析
23. 如图，在7×7的正方形网格中，A，B两点都在格点上，连结AB，请完成下列作图：

(1)、在图1中找一个格点C，使得△ABC是等腰三角形（作一个即可)：

(2)、在图2中找一个格点D，使得△ABD是以AB为直角边的直角三角形(作一个即可).

查看试题解析
24. 已知一次函数y =kx+b的图象经过点A(-1，-1）和B(1.3).

(1)、求此一次函数的表达式；

(2)、点C(-3，-5)是否在直线AB上，请说明理由.

查看试题解析
25. 如图，在△ABC中，∠ACB=90°，AC=BC，D为BC上的一点，连接AD，作CE⊥AD于点E，BF∥AC交CE的延长线于点F.

(1)、求证：AD= CF

(2)、若AC=2 $\sqrt{5}$ ，D为BC的中点，求出EF的长.

查看试题解析
26. 某工厂投资组建了日废水处理量为20吨的废水处理车间，已知该车间处理废水时每天需固定成本30元，并且每处理一吨废水还需费用8元.若该车间在无法完成当天工业废水的处理任务时，需将超出20吨的部分交给第三方企业处理。如图所示为该厂日废水处理总费用y(元)与该厂日产生的工业废水x(吨)之间的函数关系图象.

(1)、求y关于x的函数关系式：

(2)、设该厂日废水处理的平均费用为a元/吨，
①当a=10时，在图1中画出直线y=ax的图象，结合图象判断直线y=ax与日废水处理总费用y的函数图象交点个数，求交点横坐标x的值并说明它的实际意义；

②当a=t时，参照上一小题的解法，求出该厂这日产生工业废水量x的值.

查看试题解析